Конус формулы объема, площади поверхности

Для чего используется конус

Мы подробно разобрали самые простые варианты как сделать правильный конус из бумаги. Для чего используется эта поделка? Направления у нее самые различные:

• геометрических выставок;
• объемных поделок;
• изготовления маскарадных шляп.

Ваша фантазия подскажет вам, где еще может применяться конус. А мы поможем вам вдохновиться с помощью простой конусной поделки елочки.

Ёлка из конуса

Для нее потребуется:

• картон;
• бумага для подарков;
• скотч;
• декоративные предметы;
• ножницы.

В основе изделия, как вы уже поняли, лежит конус. Изготовьте его по одной из предложенных выше инструкций.

Далее работаем по схеме:

1. Полученный конус, оборачиваем бумагой для подарков. Крепим кончик материала к верхушке скотчем и аккуратно оборачиваем бумагу по фигуре. Отрезаем лишний материал.
2. Крепим концы с помощью скотча.
3. Вы не поверите, но елочка готова. Осталось ее украсить как настоящую. С этой целью могут подойти пуговицы, большие бусины и миниатюрные новогодние игрушки.

В ёлке можно сделать отверстия. И если она достаточно широка, поместите внутрь конуса новогодние огоньки. В темноте, они будут приятно мелькать, создавая приятную атмосферу.

http://ngeometry.ru/postroenie-razvertki-konusa.htmlhttp://stroyday.ru/kalkulyatory/obshhestroitelnye-voprosy/kalkulyatory-rascheta-razmerov-razvertki-konusa.htmlhttp://megamaster.info/kak-sdelat-konus-iz-bumagi/

Развертка (выкройка) конуса

• Следующий уникальный калькулятор служит для перевода экзотических единиц длины в…
• Следующий онлайн калькулятор о фунтах. Ранее он был очень популярен,…
• Следующий онлайн калькулятор может вычислить уровень жидкости в цилиндрической таре…
• Следующий онлайн калькулятор переводит температуры между разными шкалами. Помните калькулятор…
• Следующий калькулятор интересен тем, что он переводит древние российские денежные…
• Следующий калькулятор будет очень полезен тем, кто решил купить или…
• Следующий калькулятор работает очень просто, вам нужно ввести всего одно…
• Следующий онлайн калькулятор считает рост человека благодаря русской системе мер…
• Следующий онлайн калькулятор может вычислить габариты экрана телевизоров, компьютеров, проекторов,…
• Перед вами 2 калькулятора: один поможет вам подобрать формат снимков…
• Следующие 2 калькуляторы переводят заданное число плиток в квадратные метры…
• Перед вами 2 онлайн-калькулятора. Они переводят меры площади из метрической…
• Следующий необычный калькулятор переводит меры длины из русской системы в…
• Перед вами 2 калькулятора, которые предназначены для перевода мер длины…
• Следующий простенький калькулятор переводит введенную вами toC из кельвинов в…
• Следующий калькулятор предназначен для перевода кг в фунты. Также есть…
• Следующий онлайн калькулятор переводит калибр древних артиллерийских орудий из фунтов…
• Давайте вспомним калькулятор, который переводит градусы Цельсия в градусы Фаренгейта:…
• Как вы уже могли заметить на нашем сайте есть несколько…
• Следующий уникальный калькулятор переводит градусы Цельсия в градусы Фаренгейта. Наверное,…
• Следующий калькулятор умеет переводить значение угла, которое задано в градусах,…
• Следующий калькулятор делает перевод единиц измерения углов из градусов, минут,…
• Следующий калькулятор делает расчет объема сегмента цилиндра. Давайте посмотрим каким…
• Следующий онлайн-калькулятор считает объем жидкости в бочке, которая имеет цилиндрическую…
• Следующий калькулятор служит для детального подсчета суммарной работы аппарата. Вам…
• Перед вами отличный помощник для IT специалистов. С помощью данного…
• Следующий калькулятор переводит числа, записанные римскими цифрами в простые десятичные…
• Следующий калькулятор переводит скорость из м/с в км/час. Часто при…
• Начнем с истории. В 17 веке итальянским ученым Торричелли было…
• Следующий онлайн-калькулятор рассчитывает параметры горловины для цилиндрического бочки. Все работает…

hostciti.net

Презентация на тему: » Конус Понятие конуса Понятие конуса Площадь поверхности конуса Площадь поверхности конуса Усечённый конус Усечённый конус.» — Транскрипт:

1

Конус Понятие конуса Понятие конуса Площадь поверхности конуса Площадь поверхности конуса Усечённый конус Усечённый конус

2

Понятие конуса Рассмотрим окружность L с центром О и прямую ОР, перпендикулярную к плоскости этой поверхности. Через точку Р и каждую точку окружности проведём прямую. Поверхность, образованная этими прямыми, называется конической поверхностью, а сами прямые – образующими конической поверхности. L О Р

3

Точка Р называется вершиной, а прямая ОР – осью конической поверхности. Понятие конуса L О Р вершина ось конической поверхности

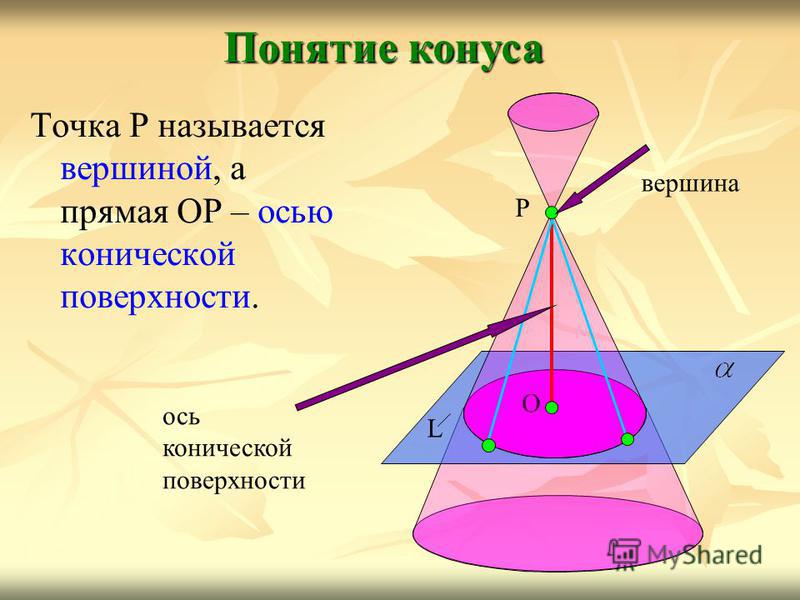
4

Тело, ограниченное конической поверхностью и кругом с границей L, называется конусом. Конус О L

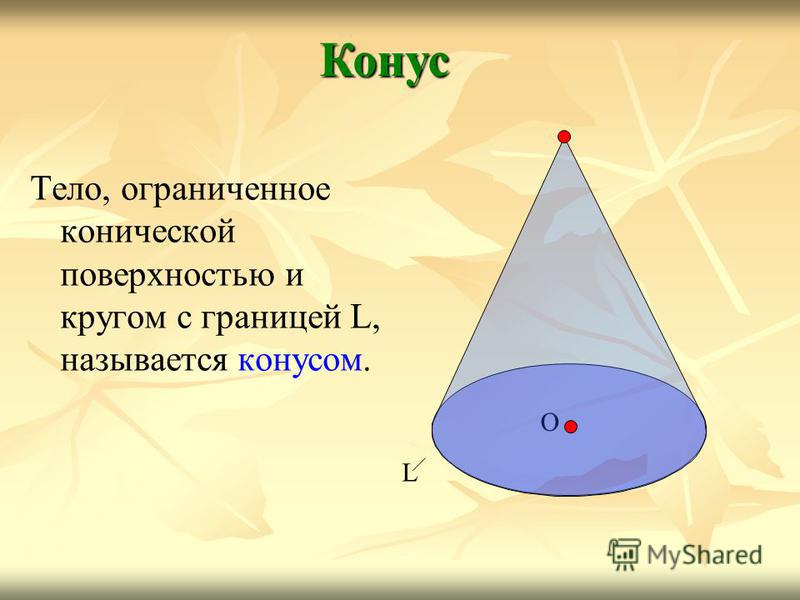
5

Круг называется основанием конуса, вершина конической поверхности – вершиной конуса, отрезки образующих, заключённые между вершиной и основанием, — образующими конуса, а образованная ими часть конической поверхности – боковой поверхностью конуса. Конус О L

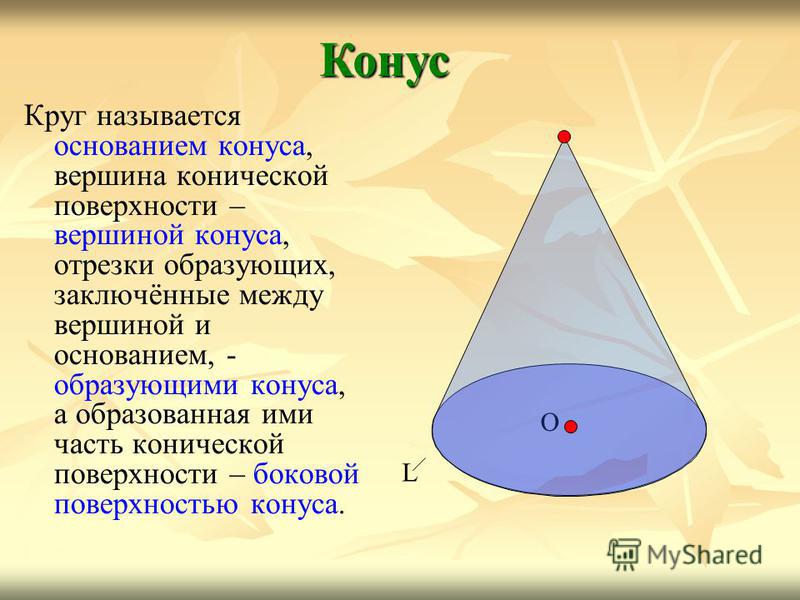
6

Конус О L Р ось конуса вершина конуса образующие конуса боковая поверхность конуса основание конуса

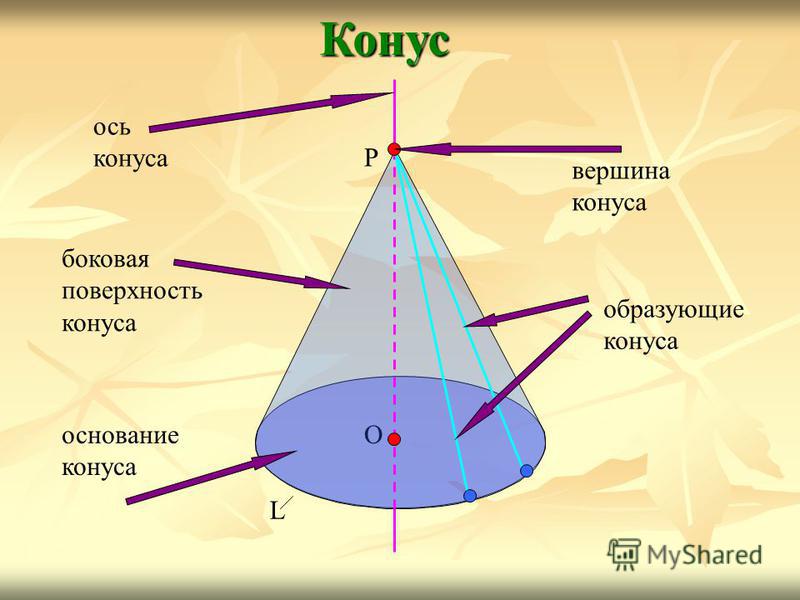
7

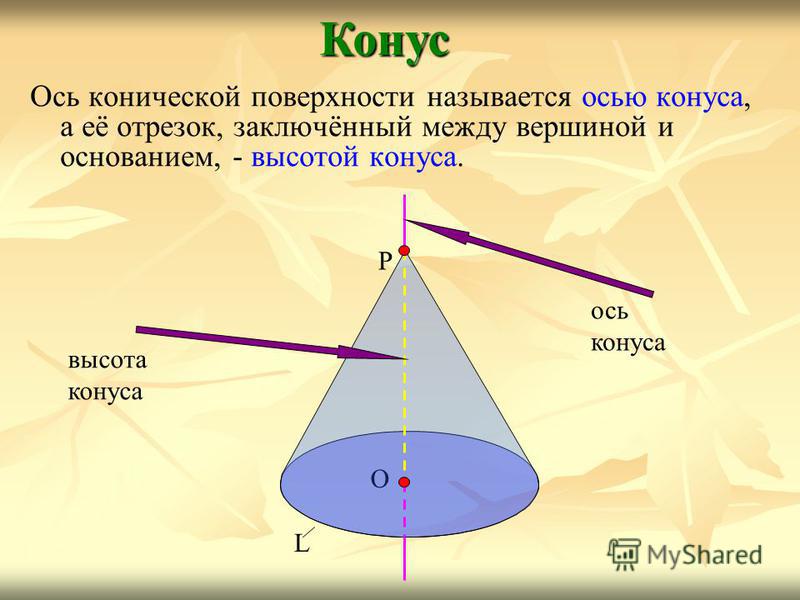
Ось конической поверхности называется осью конуса, а её отрезок, заключённый между вершиной и основанием, — высотой конуса.Конус О L Р ось конуса высота конуса

8

Конус может быть получен вращением прямоугольного треугольника вокруг одного из его катетов. Получение конуса

9

Если секущая плоскость проходит через ось конуса, то сечение представляет собой равнобедренный треугольник, основание которого – диаметр основания конуса, а боковые стороны – образующие конуса. Это сечение называется осевым. Сечение конуса О Р

10

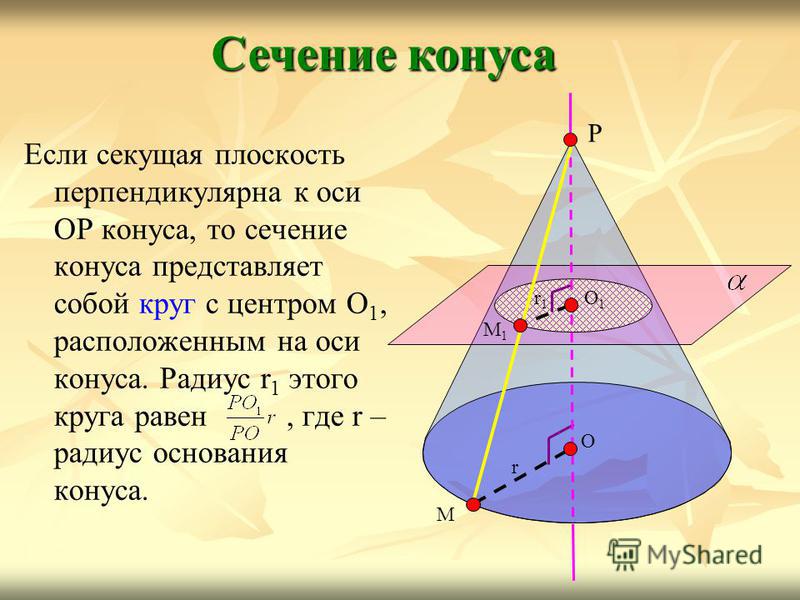
Если секущая плоскость перпендикулярна к оси ОР конуса, то сечение конуса представляет собой круг с центром О 1, расположенным на оси конуса. Радиус r 1 этого круга равен, где r – радиус основания конуса. Сечение конуса Р О М r О1О1 М1М1 r1r1

11

Проводя различные сечения одного и того же кругового конуса, причём любого, можно получить эллипс, параболу и гиперболу. При надлежащем наклоне секущей плоскости удаётся получить все типы конических сечений. Если считать, что конус не заканчивается в вершине, а простирается за неё, тогда у некоторых сечений образуются две ветви. Сечение конуса

12

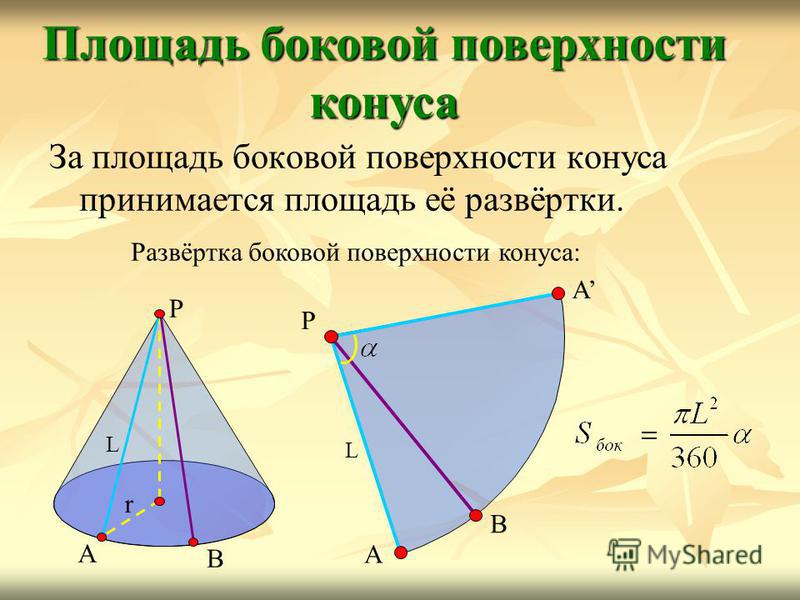
За площадь боковой поверхности конуса принимается площадь её развёртки. Площадь боковой поверхности конуса Развёртка боковой поверхности конуса: А В Р А L А В Р L r

13

Выразим через L и r. Так как длина дуги АВА равна, то, откуда Площадь боковой поверхности конуса А В Р А L Площадь боковой поверхности конуса равна произведению половины длины окружности основания на образующую.

14

Площадью полной поверхности конуса называется сумма площадей боковой поверхности и основания. Площадь полной поверхности конуса А В Р L r S кон = r 2 + rL S кон = r(r + L)

15

Возьмём произвольный конус и проведём секущую плоскость, перпендикулярную к его оси. Эта плоскость пересекается с конусом по кругу и разбивает конус на две части. Одна из частей (верхняя) представляет собой конус, а другая называется усечённым конусом. Усечённый конус Р О О1О1 конус усечённый конус

16

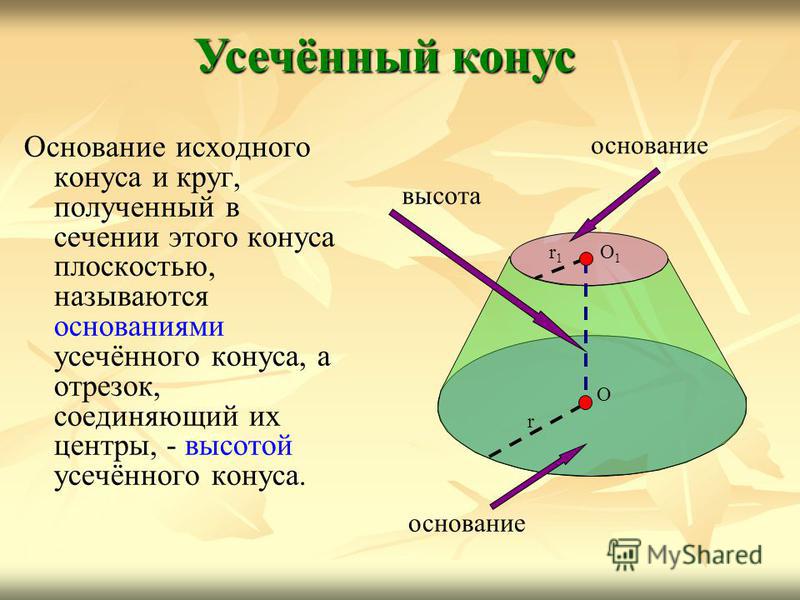
Основание исходного конуса и круг, полученный в сечении этого конуса плоскостью, называются основаниями усечённого конуса, а отрезок, соединяющий их центры, — высотой усечённого конуса. Усечённый конус О1О1 r1r1 r О основание высота

17

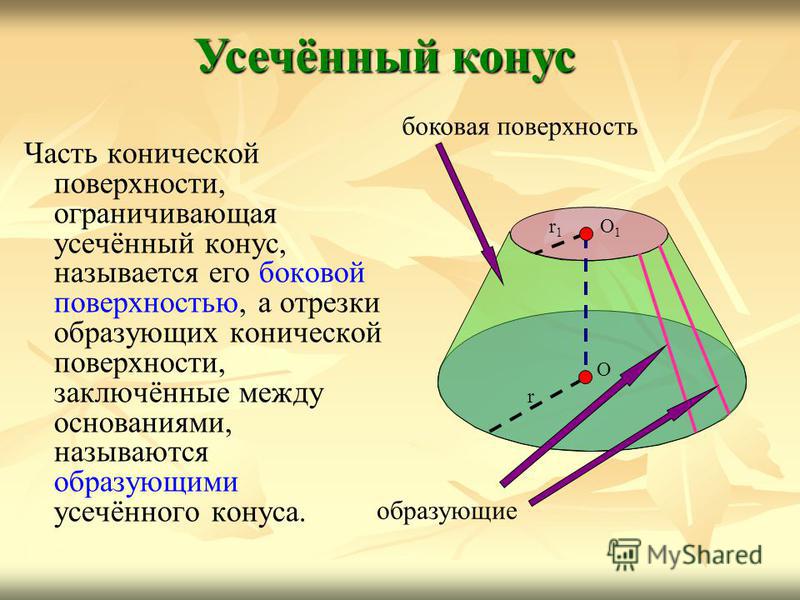
Часть конической поверхности, ограничивающая усечённый конус, называется его боковой поверхностью, а отрезки образующих конической поверхности, заключённые между основаниями, называются образующими усечённого конуса. Усечённый конус О1О1 r1r1 r О боковая поверхность образующие

18

Усечённый конус может быть получен вращением прямоугольной трапеции вокруг её боковой стороны, перпендикулярной к основаниям. Получение усечённого конуса A B C D Усечённый конус получен вращением прямоугольной трапеции ABCD вокруг стороны CD.

19

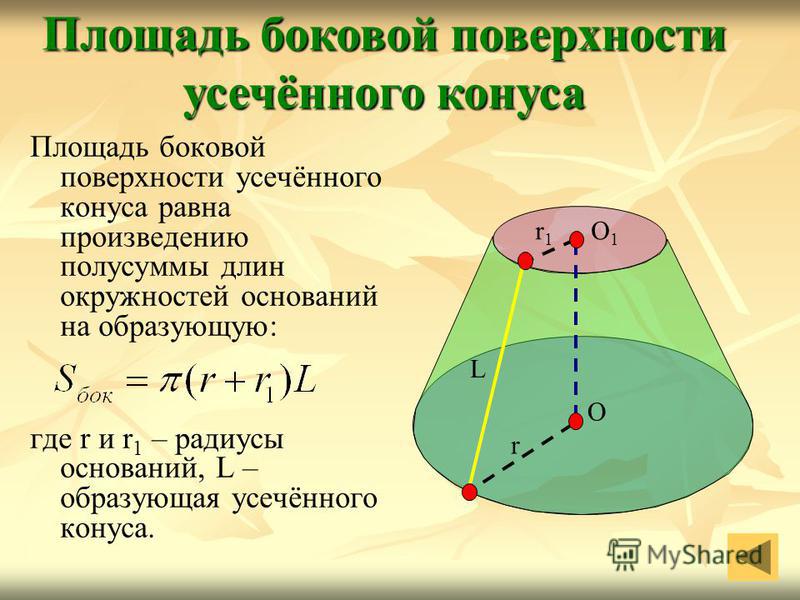
Площадь боковой поверхности усечённого конуса равна произведению полусуммы длин окружностей оснований на образующую: где r и r 1 – радиусы оснований, L – образующая усечённого конуса. Площадь боковой поверхности усечённого конуса О1О1 r1r1 r О L

История определения конуса

Геометрия как наука появилась из практических требований строительства и наблюдений за природой. Постепенно опытные знания обобщались, а свойства одних тел доказывались через другие. Древние греки ввели понятие аксиом и доказательств. Аксиомой называется утверждение, полученное практическим путем и не требующее доказательств.

В своей книге Евклид привел определение конуса как фигуры, которая получается вращением прямоугольного треугольника вокруг одного из катетов. Также ему принадлежит основная теорема, определяющая объем конуса. А доказал эту теорему древнегреческий математик Евдокс Книдский.

Другой математик древней Греции, Аполлоний Пергский, который был учеником Евклида, развил и изложил теорию конических поверхностей в своих книгах. Ему принадлежит определение конической поверхности и секущей к ней. Школьники наших дней изучают Евклидову геометрию, сохранившую основные теоремы и определения с древних времен.

Основные определения

Прямой круговой конус образован вращением прямоугольного треугольника вокруг одного катета. Как видно, понятие конуса не изменилось со времен Евклида.

Гипотенуза AS прямоугольного треугольника AOS при вращении вокруг катета OS образует боковую поверхность конуса, поэтому называется образующей. Катет OS треугольника превращается одновременно в высоту конуса и его ось. Точка S становится вершиной конуса. Катет AO, описав круг (основание), превратился в радиус конуса.

Если сверху провести плоскость через вершину и ось конуса, то можно увидеть, что полученное осевое сечение представляет собой равнобедренный треугольник, в котором ось является высотой треугольника.

Также часто требуется рассчитать площадь боковой поверхности тела вращения. Площадь боковой поверхности конуса равна произведению половины длины окружности основания и образующей конуса.

S=C*L/2=n*R*L/2

где C — длина окружности основания, l — длина образующей конуса, R — радиус основания.

Какие материалы подходят для вальцевания

Мы работаем со стальными сплавами, например, с нержавеющей сталью, цветными металлами, различными видами черных металлов, оцинкованного листа, профильного и трубного проката.

Как проходит работа?

Заключению договора предшествует обращение к нашим менеджерам и создание заявки. Для работы по проекту необходимы чертежи. Вы можете предоставить их самостоятельно или доверить это нашим мастерам. Во втором случае вам необходимо предоставить на выбор:

• эскиз;
• фотографию изделия;
• техническое задание.

Учтите, что создание чертежей не входит в основную услугу.

Следующий этап — это заключение договора, в котором будет зафиксирована конечная стоимость работ и срок их сдачи. Если заказ срочный, вы также можете указать это, и мы максимально сократим сроки работы.

После этого начинается работа наших специалистов. Мы изготавливаем изделие, соответствующее предоставленным параметрам. Мы используем высокотехнологичное оборудование и контролируем производство на каждом этапе.

Когда вальцовка металла завершена, мы доставляем готовый продукт, и вы осуществляете его прием.

Заказывайте наши услуги с помощью заявки на сайте или позвоните нашим специалистам по телефонам в Москве +7(495)730-222-4, +7(985)540-01-00.

Информация

Математика является основой всего, что нас окружает. Она особенно важна в таких сферах деятельности, как технологии, строительство и техника. Еще в средней школе дети начинают изучать различные математические законы, формулы и много другое. Одной из важнейших формул выступает формула, по которой находится объем конуса. Данная формула применяется специалистами во многих видах деятельности. Также часто применяется формула, по которой вычисляют объем усеченного конуса.

В профессиональной деятельности у инженера или строителя нет права на допущение ошибки. Это связанно с тем, что их ошибка может стоить кому-нибудь жизни. Для того, чтобы облегчить и обезопасить расчеты в профессиональной деятельности, был создан такой инструмент, как онлайн-калькулятор. Он позволяет совершать вычислительные действия любых показателей, вводя исходные значения в формулу. Калькулятор выдает предельно точный результат и исключает возможность возникновения ошибки в процессе вычислений.

Для вычислений в данном калькуляторе используется три основные формулы:

1. Формула для вычисления объема конуса через радиус и высоту.
2. Формула отвечающая на вопрос « Как найти объем конуса через площадь его основания и высоту?».
3. Последняя формула позволяет найти объем усеченного конуса, зная радиус и высоту.

Используя наш онлайн-калькулятор, Вы получаете следующие выгоды:

• Точность и достоверность результатов проведенного вычисления, которая полностью исключает ошибки в процессе осуществления профессиональной деятельности.
• Экономия времени, благодаря исключению необходимости самостоятельных расчетов.
• Интерфейс нашего калькулятора разработан максимально простым и удобным.

Для того, чтобы использовать наш онлайн-калькулятор, необходимо совершить следующие действия:

• Выбрать вид конуса (прямой или усеченный).
• Ввести исходные данные (высота, радиус, площадь).
• Введя необходимы данные калькулятор автоматически сообщит, что объем конуса равен тому или иному значению.

Решение задачи

Даже простая задача о том, как изготовить ведро определенного объема, требует знаний. Например, необходимо рассчитать размеры ведра, чтобы оно имело объем 10 литров.

Дано:

V=10 л=10 дм3;

R₁=15 см;

R₂=25 см.

Развертка конуса имеет вид, схематически приведенный на рисунке 3.

L — образующая конуса.

Чтобы узнать площадь поверхности ведра, которая вычисляется по следующей формуле:

S=n*(R₁+R₂)*L,

необходимо вычислить образующую. Ее находим из величины объема V=n*(R₁2+R₂2+R₁*R₂)*H/3.

Отсюда H=3V/n*(R₁2+R₂2+R₁*R₂).

Усеченный конус образуется вращением прямоугольной трапеции, в которой боковая сторона является образующей конуса.

L2=(R_2-R₁)2+H2.

Теперь у нас имеются все данные, чтобы построить чертеж ведра.

Как сделать конус для елки своими руками?

Для изготовления такой ели потребуется картон, обычная и цветная бумага, ножницы и клей. И разумеется — побольше фантазии. Наилучший материал для изготовления конуса-основы для ёлки – картон. Только для маленьких нежных и воздушных ёлочек, конус можно делать из бумаги.

Конус сворачивается двумя способами

Лист картона скручивается самым элементарным образом, наподобие кулька для семечек. Лишние края, выступающие из широкой части конуса, обрезаются, а сам конус склеивается. Нижний край обрезается так, чтобы конус стоял ровно и не косился на одну сторону.

На картоне вычерчивается ровный круг (лучше циркулем, но можно обвести тарелку или таз, правда в этом случае трудно будет найти центр) и делится на четыре равные части. Одна из этих частей вырезается, после чего из оставшейся фигуры скручивается конус необходимой сбежистости. Края закрепляются клеем. Конус уравновешивается, аналогично первому способу.

После этого можно делать «хвою» или «ветки» любым выбранным способом, а затем украшать гирляндами лампочек, маленькими игрушками и т.д. Такие ёлочки подходят не только для украшения дома, но и для новогоднего подарка.

Расчет развертки конуса.

Возьмем вертикальную и горизонтальную проекции конуса (рис. 1, а). Вертикальная проекция конуса будет иметь вид треугольника, основание которого равно диаметру окружности, а стороны равны образующей конуса. Горизонтальная проекция конуса будет изображаться окружностью. Если задана высота конуса Н, то длина образующей определяется по формуле:

т. е. как гипотенуза прямоугольного треугольника.

Обвернем картоном поверхность конуса. Развернув картон снова в одну плоскость (рис. 1, б), получим сектор, радиус которого равен длине образующей конуса, а длина дуги равна длине окружности основания конуса. Полную развертку боковой поверхности конуса выполняют следующим образом.

Рис. 1. Развертка конуса:а — проекция; б — развертка.

Угол развертки конуса.

Принимая за радиус образующую конуса (рис. 1, б), на металле вычерчивают дугу, на которой затем откладывают отрезок дуги КМ

, равный длине окружности основания конуса2πr . Длине дуги в2πr соответствует уголα , величина которого определяется по формуле:

г — радиус окружности основания конуса;

l — длина образующей конуса.

Построение развертки сводится к следующему. На длине ранее вычерченной дуги откладывается не часть дуги КМ

, что практически является невозможным, а хорда, соединяющая концы этой дуги и соответствующая углуα . Величина хорды для заданного угла находится в справочнике или проставляется на чертеже.

Найденные точки КМ

соединяются с центром окружности. Круговой сектор, полученный в результате построения, будет развернутой боковой поверхностью конуса.

Информация

Математика является основой всего, что нас окружает. Она особенно важна в таких сферах деятельности, как технологии, строительство и техника. Еще в средней школе дети начинают изучать различные математические законы, формулы и много другое. Одной из важнейших формул выступает формула, по которой находится объем конуса. Данная формула применяется специалистами во многих видах деятельности. Также часто применяется формула, по которой вычисляют объем усеченного конуса.

В профессиональной деятельности у инженера или строителя нет права на допущение ошибки. Это связанно с тем, что их ошибка может стоить кому-нибудь жизни. Для того, чтобы облегчить и обезопасить расчеты в профессиональной деятельности, был создан такой инструмент, как онлайн-калькулятор. Он позволяет совершать вычислительные действия любых показателей, вводя исходные значения в формулу. Калькулятор выдает предельно точный результат и исключает возможность возникновения ошибки в процессе вычислений.

Для вычислений в данном калькуляторе используется три основные формулы:

1. Формула для вычисления объема конуса через радиус и высоту.
2. Формула отвечающая на вопрос « Как найти объем конуса через площадь его основания и высоту?».
3. Последняя формула позволяет найти объем усеченного конуса, зная радиус и высоту.

Используя наш онлайн-калькулятор, Вы получаете следующие выгоды:

• Точность и достоверность результатов проведенного вычисления, которая полностью исключает ошибки в процессе осуществления профессиональной деятельности.
• Экономия времени, благодаря исключению необходимости самостоятельных расчетов.
• Интерфейс нашего калькулятора разработан максимально простым и удобным.

Для того, чтобы использовать наш онлайн-калькулятор, необходимо совершить следующие действия:

• Выбрать вид конуса (прямой или усеченный).
• Ввести исходные данные (высота, радиус, площадь).
• Введя необходимы данные калькулятор автоматически сообщит, что объем конуса равен тому или иному значению.

Колпак на дымоход своими руками

Хозяева домов зачастую прибегают к использованию элементов в виде различных колпаков и зонтов, служащих, как это кажется на первый взгляд, для украшения дымовых труб. В то же время такие насадки не только улучшают эстетическое восприятие строения, но и обеспечивают полезную функциональность. Обычно так называемый козырек для дымохода изготавливается собственными силами, так как для этого не требуется серьезных знаний и умений. Хотя наряду с простой конструкцией этих элементов встречаются достаточно замысловатые поделки, которые проблематично соорудить без соответствующего опыта.

Конструктивные особенности

Колпак на дымоход представляет собой устройство, предназначенное для защиты трубы от попадания влаги. Внешний вид таких козырьков может быть различен, что имеет зависимость как от предпочтений хозяина дома, так и от конфигурации трубы.

Колпаки на трубу дымохода включают в себя:

• зонтик – устанавливаемая на вершине колпака защита от осадков, посторонних предметов и проникновения птиц, внешний вид которой имеет форму пирамиды, конуса или соответствует другой геометрии;
• фартук – часть колпака, отвечающая за защиту верха трубы от стекающей с зонтика воды. Обычно установка этого элемента производится при оснащении прямоугольной или квадратной трубы. В результате гарантируется увеличение срока службы дымохода, так как удается практически исключить вероятность появления коррозии и грибка;
• кронштейны – крепежные элементы, представляющие собой металлические полоски, которые позволяют соединить козырек и фартук. Непосредственное крепление в данном случае производится за счет использования сварки.

Имейте в виду! Собрать колпак для дымохода вполне реально самому, но только в том случае, если вы хотите установить достаточно простой флюгарок. Модели, отличающиеся большей сложностью в плане конструктивных особенностей, гораздо выгоднее заказать или купить.

При наличии выбора лучше всего отдать предпочтение тем моделям, которые оборудованы открывающейся крышкой. Это позволит проводить профилактический осмотр дымохода и его чистку без каких-либо проблем, что связано с комфортом доступа.

Колпак на дымоход долгого срока использования может быть изготовлен только из железа, устойчивого к коррозии: оцинкованная сталь, алюминий и медь. В последнем случае предлагаемый металл обладает ярко выраженным декоративным характером, так как его переливы на солнце могут придать вашем дому определенную респектабельность.

Одевают оголовок на трубу дымохода чтобы гасить искры. Это одно из его предназначений. Поэтому качество железа должно быть хорошим, тем самым оно долго не прогорит.

Виды

В связи с тем, что дымоходы отличаются разнообразием форм и размеров, производители колпаков также предлагают широкий ассортимент продукции. Если вы решите украсить свое жилище и продлить срок жизни дымохода, то придется выбирать среди большого ассортимента флюгарок:

1. Стандартные – зонт на дымоход в виде пирамидки, для изготовления которой используется листовой металл, а крепление к фартуку осуществляется посредством кронштейнов.
2. Четырехскатные – устанавливается преимущественно на прямоугольные трубы, выполненные из кирпича. По форме соотносится с вальмовой крышей с четырьмя скатами.
3. С полукруглым зонтиком – визуально отличается красотой, но обеспечивает недостаточную тягу. Преимущественно используется для установки на дымоходах домов, которые построены по европейским стандартам.
4. Плоские – часто можно встретить на зданиях в стиле модерн. Имеет прямоугольную форму и отличается таким недостатком, как повышенная нагрузка на кронштейны, что в некоторых случаях приводит к их деформации. Это связано с плоской крышей колпака, которая не дает возможность скатываться снегу. Данный факт определяет возникновение упомянутой проблемы.
5. Круглые с конусообразным зонтиком – модели без капельника, устанавливаемые на выполненные из нержавейки дымоходы круглого сечения.

Практическое применение

У школьников часто возникает вопрос о том, зачем учить, как рассчитывать объем разных геометрических тел, в том числе конуса.

А инженеры-конструкторы постоянно сталкиваются с необходимостью рассчитать объем конических частей деталей механизмов. Это наконечники сверл, части токарных и фрезерных станков. Форма конуса позволят сверлам легко входить в материал, не требуя первоначальной наметки специальным инструментом.

Объем конуса имеет куча песка или земли, высыпанная на землю. При необходимости, проведя несложные измерения, можно рассчитать ее объем. У некоторых вызовет затруднение вопрос о том, как узнать радиус и высоту кучи песка. Вооружившись рулеткой, измеряем окружность холмика C. По формуле R=C/2n узнаем радиус. Перекинув веревку (рулетку) через вершину, находим длину образующей. А вычислить высоту по теореме Пифагора и объем не составит труда. Конечно, такой расчет приблизителен, но позволяет определить, не обманули вас, привезя тонну песка вместо куба.

Некоторые здания имеют форму усеченного конуса. Например, Останкинская телебашня приближается к форме конуса. Ее можно представить состоящей из двух конусов, поставленных друг на друга. Купола старинных замков и соборов представляют собой конус, объем которого древние зодчие рассчитывали с удивительной точностью.

Если внимательно присмотреться к окружающим предметам, то многие из них являются конусами:

• воронки-лейки для наливания жидкостей;
• рупор-громкоговоритель;
• парковочные конусы;
• абажур для торшера;
• привычная новогодняя елочка;
• духовые музыкальные инструменты.

Как видно из приведенных примеров, умение рассчитать объем конуса, площадь его поверхности необходимо в профессиональной и повседневной жизни. Надеемся, что статья придет вам на помощь.

Создаем новогоднюю елку

Из готового бумажного конуса можно создать отличное новогоднее украшение в виде елочки. Материалы при этом используются самые разнообразные, но общая система изготовления остается общей.

• На бумажный конус наклеивается скотч или пищевая пленка.
• Поверх них, с помощью ПВА или другого подходящего клея, прикрепляются толстые шерстяные нитки.
• После того, как они хорошо засохнут, нужно вынуть из них конус. Нити должны сохранить его форму.
• Останется только добавить элементы для украшения. Это могут быть небольшие вязаные шарики, звездочки из блестящей бумаги или любые другие материалы, оказавшиеся под рукой.

Для создания новогодней елочки можно воспользоваться совершенно другой техникой. На помощь придет папье-маше, с помощью которой можно тоже сделать бумажный конус. Конечно, материала и времени потребуется гораздо больше, но и готовая конструкция получится прочной и статной.

• Для работы потребуются газетные или журнальные обрезки. Подойдет практически любая бумага. Также необходима основа. Можно взять любой пластиковый конус, например – из детских игрушек. Он не пострадает при процессе изготовления.
• Выбранную основу обмазывают ПВА и накладывают на неё слой бумаги. Когда он подсохнет, можно наносить следующий. Таким образом процесс продолжается, пока не наберется достаточная толщина.
• Теперь нужно извлечь основу. Иногда для этого приходится разрезать фигуру.
• Затем вместо основы можно пометить внутрь стержень, который будет выполнять роль каркаса.

Остается лишь склеить разрезанные половинки обратно, и можно приступать к декорированию будущей елки. Например, её реально покрасить или обмотать нитками, как на фото ниже. Такая схема позволит создать любые варианты елочек, в зависимости от желания и имеющейся основы.