Как сделать ровный конус из бумаги. как сделать развертку

Как сделать конус из бумаги своими руками?

Материалы для создания полностью определяются тем, зачем делается конус. Самые простые варианты из обычного листа бумаги можно даже не склеивать – достаточно скрепить каким-нибудь зажимом. Если же предстоит соорудить красивую елочную игрушку или элемент декора, то лучше найти подходящую цветную бумагу или картон.

Для создания ровного конуса понадобится круглый лист.

Его можно сделать разными способами, например – вырезать из обычного, формата А4, обозначив требуемую зону циркулем. В случае, если циркуля под рукой не оказалось, стоит воспользоваться карандашом и веревкой. Нить должна равняться радиусу будущего круга. Её придерживают пальцем в центре листа в натянутом состоянии, а карандашом обводится окружность.

Как сделать конус из бумаги своими руками:

• На готовом круге нужно начертить две линии, чтобы получится крест, разделяющий лист на четыре ровные части.
• Затем одну из четвертей отрезают.
• Остается лишь сложить нужную форму и закрепить её с помощью клея или прищепок.

После этого конус готов, но, при желании, можно сделать для него дно. Для этого получившуюся фигуру ставят на лист бумаги. По ней обводят круг, но перед вырезанием к форме добавляют ещё примерно сантиметр. Из этого расстояния нужно создать зубчики, с помощью которых дно будет крепиться к конусу. Их промазывают клеем и прикрепляют.

При работе с тонкой бумагой можно делать конус из обычного прямоугольного листа. Для этого он закручивается, как показано на фото ниже, а затем лишний край отрезается. Иногда его можно использовать для создания основы конуса, или же бывает достаточным просто загнуть его вовнутрь.

Видео гибки конусной обечайки

После сборки проверяется сварочный зазор и выполняются сварочные прихватки (рис.21). Параметры прихваток приведены в таблице 2. Заходные и выводные планки применяются для обеспечения качественного сварного шва по торцам обечайки.

При сборке обечаек используются роликовые стенды (рис.22) и кантователи. Сварку кольцевых и продольных швов обечаек производят ручным способом, механизированным способом или с применением сварочных роботов. Для ликвидации остаточных напряжений в сварных швах обечайки подвергают термообработке в шахтных печах. После сварки производится калибровка обечайки на вальцах — прокатка ее в несколько заходов. При окончательном контроле изготовленных обечаек проверяют их геометрические размеры, отсутствие деформаций и поверхностных дефектов детали.

Установлен сертификат профессионализма, соответствующий занятию промышленного кипятильника, профессиональной семьи тяжелой промышленности и металлических конструкций, который будет иметь официальный характер и действительность на всей территории страны.

Сертификат профессионализма. Аккредитация учебного контракта. Только переходное положение. Адаптация к национальному учебному и профессиональному плану внедрения. Министр труда и социальных дел настоящим уполномочен издавать такие положения, которые могут потребоваться для осуществления этого Королевского указ.

Более подробно об изготовлении отдельных видов обечаек, читайте в разделах «Вентиляция», «Водосток» и «Для гибки металла».

Вальцовка обечаек – важнейший технологический процесс, без которого нельзя даже представить производство цилиндрических деталей. Рассмотрим более подробно его особенности, технологию и используемый инструмент.

Этот Королевский указ вступает в силу на следующий день после его опубликования в Официальном государственном бюллетене. В Мадриде 24 января. Министр труда и социальных дел. Профессиональный профиль профессии. Для строительства различных элементов используются режущие и формовочные машины, а также электросварочное оборудование, а также организует рабочее оборудование для получения продуктов в условиях безопасности и требуемых качественных характеристик. Построить металлические конструкции.

Построить наборы цилиндрических каналов. Компетентность 1: сборка металлоконструкций. Компетентность 2: построение наборов цилиндрических трубопроводов. Компетентность 3: построение конусов и бункеров. Наблюдение при формовании в горячем состоянии не превышает предельную температуру молекулярной структуры материала.

Построение развертки конуса на бумаге

Для выполнения этой задачи понадобится лист бумаги, карандаш, транспортир, линейка и циркуль.

В первую очередь начертим прямоугольный треугольник со сторонами 3 см, 4 см и 5 см. Его вращение вокруг катета в 3 см даст искомый конус. У фигуры r = 3 см, h = 4 см, g = 5 см.

Построение развертки начнем с рисования циркулем окружности радиусом r. Ее длина будет равна 6*pi см. Теперь рядом с ней нарисуем еще одну окружность, но уже радиусом g. Ее длина будет соответствовать 10*pi см. Теперь нам нужно от большой окружности отрезать круговой сектор. Его угол φ равен:

Теперь откладываем транспортиром этот угол на окружности с радиусом g и проводим два радиуса, которые будут ограничивать круговой сектор.

Таким образом, мы построили развертку конуса с указанными параметрами радиуса, высоты и образующей.

Исходный полный конус

Прежде чем говорить об усеченном объекте и его характеристиках, следует рассмотреть исходную фигуру, из которой он получается.

Пусть имеется некоторая замкнутая кривая, лежащая в произвольной плоскости. Это может быть окружность, эллипс или любая другая линия с плавными перегибами. Пусть также существует отрезок, который не лежит в плоскости указанной замкнутой кривой. Если в пространстве зафиксировать некоторую точку, а затем соединить ее с любой точкой на кривой, то получится образующая будущего конуса. Если теперь ее перемещать вдоль замкнутой кривой одним своим концом, в то время как другой конец будет зафиксированным в точке, то она опишет коническую поверхность.

Это геометрическое построение позволяет получить объемную фигуру конус, которая состоит из следующих элементов:

1. Вершина — зафиксированная точка в пространстве, которая не лежит в плоскости замкнутой кривой.
2. Коническая поверхность, образованная в результате перемещения отрезка — образующей, или генератрисы.
3. Основание — часть плоскости, ограниченная исходной замкнутой кривой. Последняя является направляющей, или директрисой, для образующей.

Существующие виды

В геометрии известны несколько видов конуса. Каждый из них определяется характером директрисы и расположением относительно нее генератрисы. Выделяют следующие виды фигуры:

1. Круглый прямой. В его основании лежит круг, а высота (длина перпендикуляра, опущенного из вершины) соединяет центр окружности и вершину.
2. Эллиптический прямой. В его основании находится эллипс, а проекция вершины попадает точно в центр основания.
3. Наклонный произвольного вида. Высота в этом конусе всегда меньше, чем длина отрезка, соединяющего вершину и геометрический центр основания.

Круглая прямая фигура

Получить этот конус несложно. Необходимо взять прямоугольный треугольник, поставить его на один из катетов и вращать вокруг второго катета, который будет являться осью, а его длина — высотой для объемной фигуры. Катет, на котором стоит треугольник, является радиусом круглого основания конуса.

С полученной фигурой легко работать при решении геометрических задач, поскольку для нее существуют довольно простые формулы для площади поверхности и объема.

Площадь S фигуры состоит из двух частей: основания и боковой поверхности. С помощью простых геометрических рассуждений можно показать, что сумма этих частей выражается в виде такой формулы: S = pi*r2 + pi*g*r, где число pi=3,14, r — радиус окружности в основании, g — длина генератрисы. В разрезе на плоскости коническая поверхность представляет собой сектор круга радиусом g.

Как построить развертку поверхности прямого усеченного конуса

Делим основание конуса на 12 равных частей (вписываем правильную пирамиду). Данные элементы построения уже готовы из чертежа «Сечение конуса плоскостью частного положения».

Строим развертку боковой поверхности конуса, которая представляет собой круговой сектор. Центр его радиуса принимается за вершину конуса, а величина радиуса кругового сектора конуса равна длине образующей конуса, а длина дуги сектора равна длине окружности основания конуса. На дугу сектора переносим 12 хорд, которые определят ее длину, а также угол кругового сектора.

К центральной точке дуги сектора боковой развертки усеченного конуса пристраиваем основание конуса. Его основание проецируется в натуральную величину на горизонтальную плоскость проекции.

На развертке конуса к его основанию пристраиваем натуральную величину сечения.

Две крайние образующие конуса, которые формируют его основной контур, проецируются на фронтальную плоскость проекции в натуральную величину, поэтому их можно сразу переносить на развертку боковой поверхности конуса. Так как часть его срезана фронтально проецирующей плоскостью, то перенесем на развертку конуса только крайнюю правую усеченную образующую. Остальные усеченные образующие конуса проецируются на фронтальную плоскость проекций с искажением. Их натуральную величину находят способом вращения вокруг оси конуса до положения, параллельного фронтальной плоскости проекций.

Сам принцип нахождения натуральных величин образующих усеченного конуса сводится к тому, что проводят из точек пересечения образующих с плоскостью горизонтальную прямую до крайней правой (левой) образующей и на ней отмеряют натуральные их величины. Все действия проводят на фронтальной плоскости проекции.

На каждой образующей, лежащей на развертке боковой поверхности конуса, откладываем действительные длины усеченных образующих. Полученные точки соединяем плавной кривой линией команда Сплайн в Автокад.

Мы выполнили задачу начертательной геометрии на построение развертки усеченного конуса, но чтобы не возникло проблем во время ее защиты (когда я обучался, каждая курсовая по начертательной геометрии защищалась), еще раз рассмотрим принцип вращения для нахождения натуральной величины усеченной образующей конуса.

«Их натуральную величину находят способом вращения вокруг оси конуса до положения, параллельного фронтальной плоскости проекций.» Когда мы вращаем образующую прямого конуса до положения параллельного фронтальной плоскости проекции, то ее траектория описывает дугу на горизонтальной плоскости проекции, а на фронтальной прямую!

Вы можете не проводить линии связи с горизонтальной плоскости проекции на фронтальную, ведь очевидно, что точка будет лежать на крайней основной образующей контура конуса для каждой образующей при нахождении ее натуральной величины. Поэтому сам принцип вращения по нахождению натуральной величины образующих конуса сводится к проведению из точек усеченных образующих горизонтальной прямой до основной образующей контура конуса.

В видеоуроке очень наглядно и подробно показан принцип построения развертки прямого усеченного конуса.

Презентация на тему: » Конус Понятие конуса Понятие конуса Площадь поверхности конуса Площадь поверхности конуса Усечённый конус Усечённый конус.» — Транскрипт:

1

Конус Понятие конуса Понятие конуса Площадь поверхности конуса Площадь поверхности конуса Усечённый конус Усечённый конус

2

Понятие конуса Рассмотрим окружность L с центром О и прямую ОР, перпендикулярную к плоскости этой поверхности. Через точку Р и каждую точку окружности проведём прямую. Поверхность, образованная этими прямыми, называется конической поверхностью, а сами прямые – образующими конической поверхности. L О Р

3

Точка Р называется вершиной, а прямая ОР – осью конической поверхности. Понятие конуса L О Р вершина ось конической поверхности

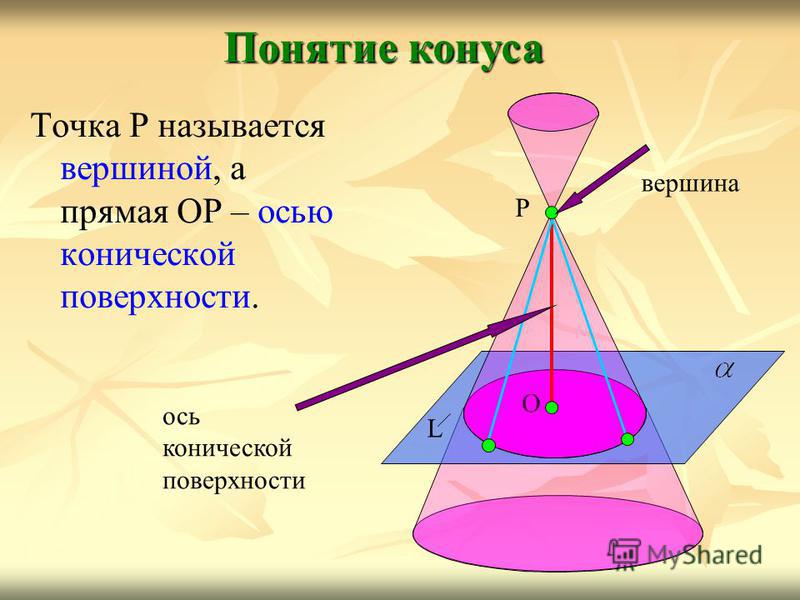
4

Тело, ограниченное конической поверхностью и кругом с границей L, называется конусом. Конус О L

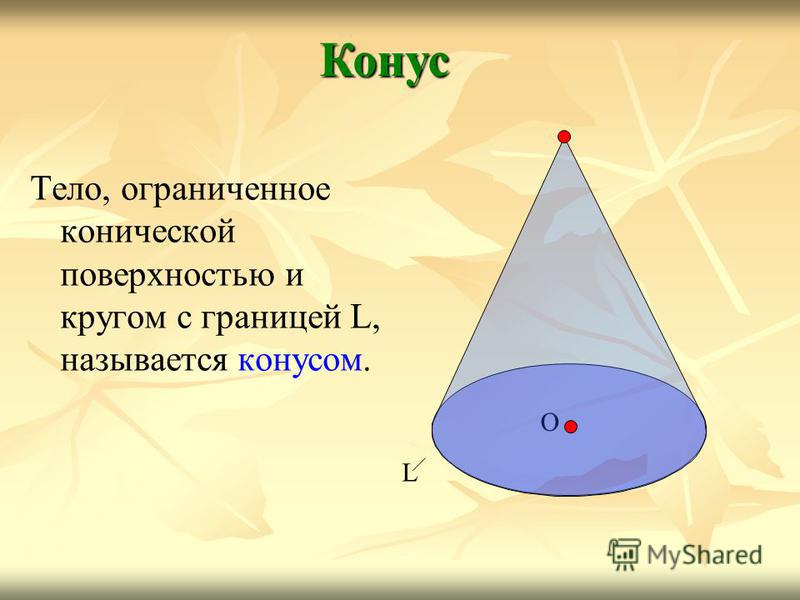
5

Круг называется основанием конуса, вершина конической поверхности – вершиной конуса, отрезки образующих, заключённые между вершиной и основанием, — образующими конуса, а образованная ими часть конической поверхности – боковой поверхностью конуса. Конус О L

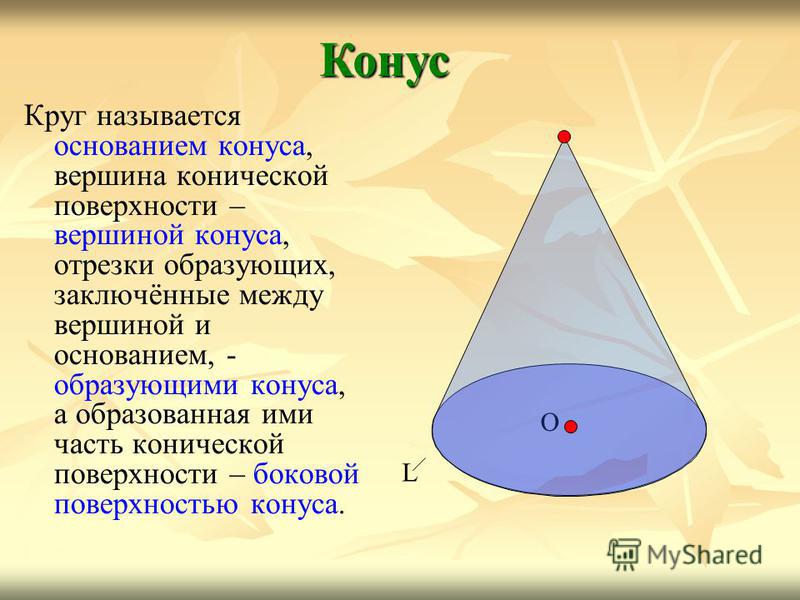
6

Конус О L Р ось конуса вершина конуса образующие конуса боковая поверхность конуса основание конуса

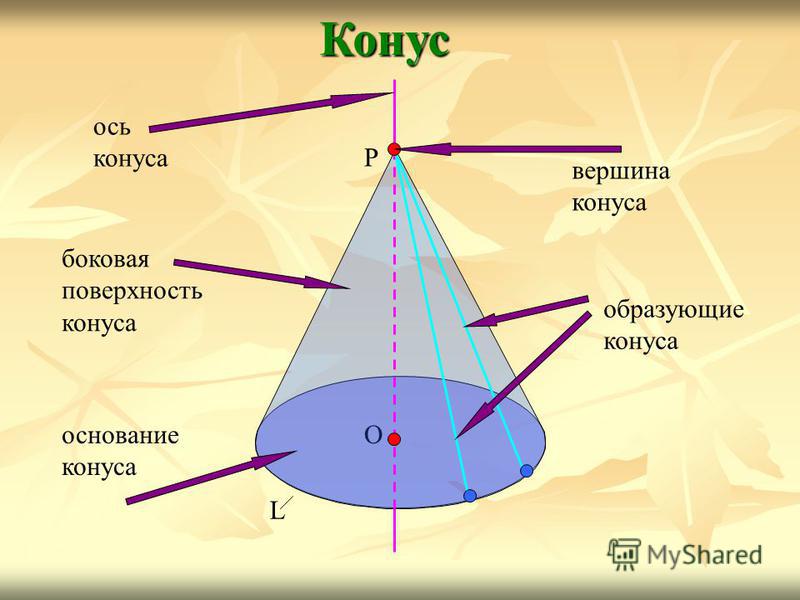
7

Ось конической поверхности называется осью конуса, а её отрезок, заключённый между вершиной и основанием, — высотой конуса.Конус О L Р ось конуса высота конуса

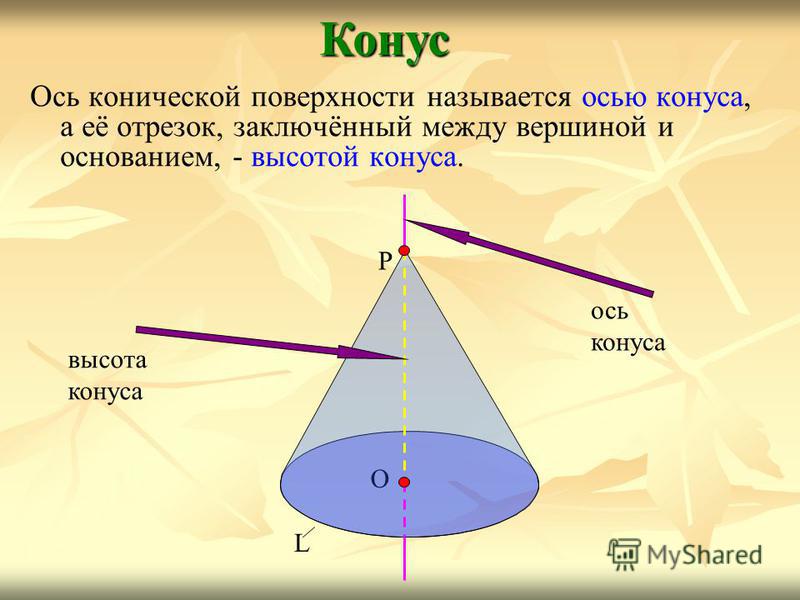
8

Конус может быть получен вращением прямоугольного треугольника вокруг одного из его катетов. Получение конуса

9

Если секущая плоскость проходит через ось конуса, то сечение представляет собой равнобедренный треугольник, основание которого – диаметр основания конуса, а боковые стороны – образующие конуса. Это сечение называется осевым. Сечение конуса О Р

10

Если секущая плоскость перпендикулярна к оси ОР конуса, то сечение конуса представляет собой круг с центром О 1, расположенным на оси конуса. Радиус r 1 этого круга равен, где r – радиус основания конуса. Сечение конуса Р О М r О1О1 М1М1 r1r1

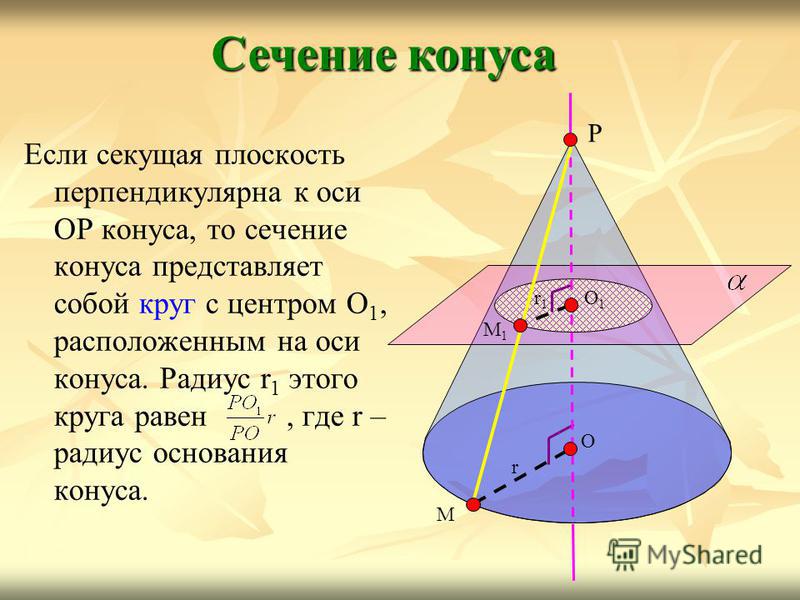
11

Проводя различные сечения одного и того же кругового конуса, причём любого, можно получить эллипс, параболу и гиперболу. При надлежащем наклоне секущей плоскости удаётся получить все типы конических сечений. Если считать, что конус не заканчивается в вершине, а простирается за неё, тогда у некоторых сечений образуются две ветви. Сечение конуса

12

За площадь боковой поверхности конуса принимается площадь её развёртки. Площадь боковой поверхности конуса Развёртка боковой поверхности конуса: А В Р А L А В Р L r

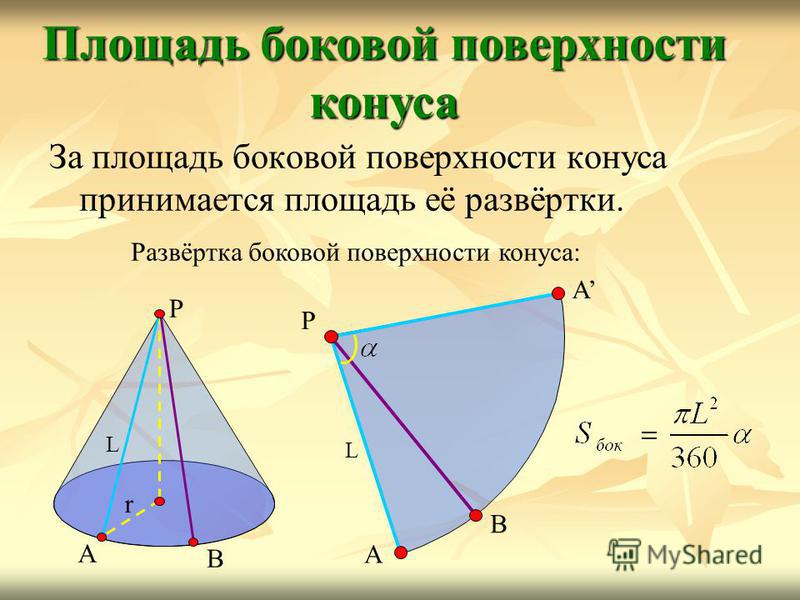
13

Выразим через L и r. Так как длина дуги АВА равна, то, откуда Площадь боковой поверхности конуса А В Р А L Площадь боковой поверхности конуса равна произведению половины длины окружности основания на образующую.

14

Площадью полной поверхности конуса называется сумма площадей боковой поверхности и основания. Площадь полной поверхности конуса А В Р L r S кон = r 2 + rL S кон = r(r + L)

15

Возьмём произвольный конус и проведём секущую плоскость, перпендикулярную к его оси. Эта плоскость пересекается с конусом по кругу и разбивает конус на две части. Одна из частей (верхняя) представляет собой конус, а другая называется усечённым конусом. Усечённый конус Р О О1О1 конус усечённый конус

16

Основание исходного конуса и круг, полученный в сечении этого конуса плоскостью, называются основаниями усечённого конуса, а отрезок, соединяющий их центры, — высотой усечённого конуса. Усечённый конус О1О1 r1r1 r О основание высота

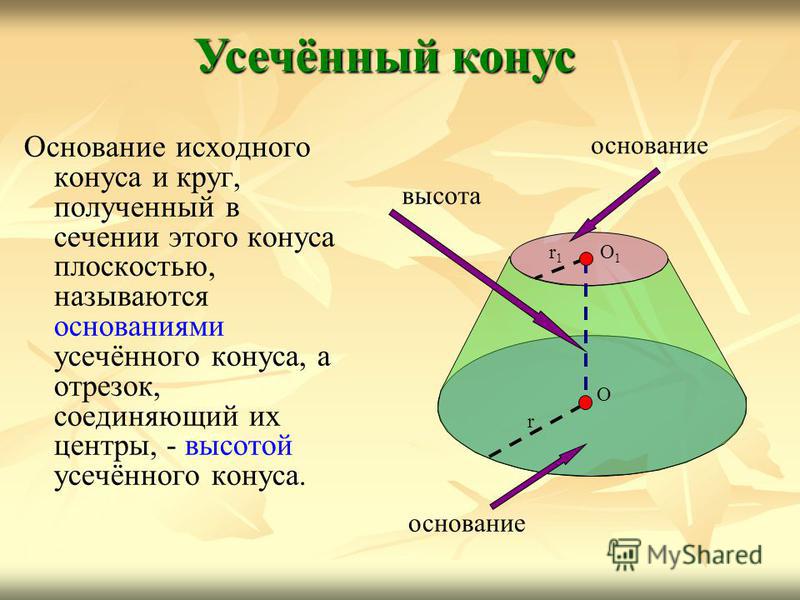
17

Часть конической поверхности, ограничивающая усечённый конус, называется его боковой поверхностью, а отрезки образующих конической поверхности, заключённые между основаниями, называются образующими усечённого конуса. Усечённый конус О1О1 r1r1 r О боковая поверхность образующие

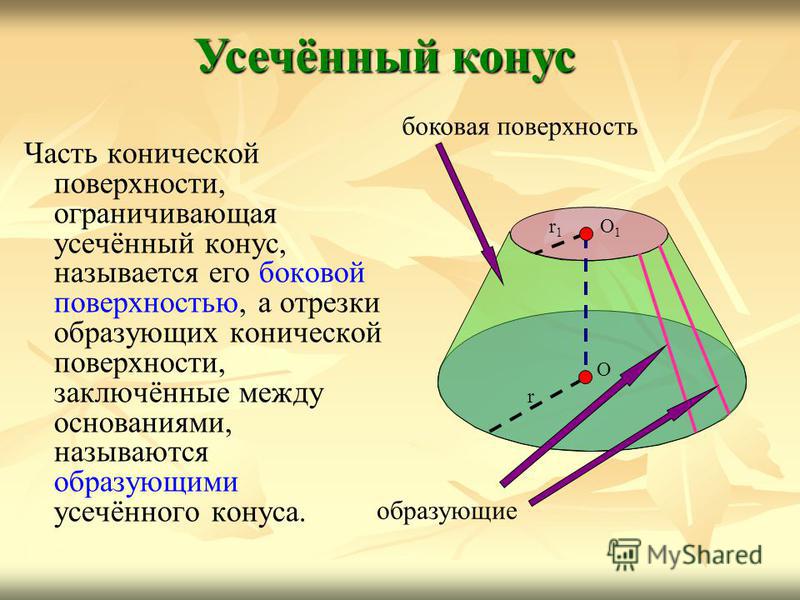
18

Усечённый конус может быть получен вращением прямоугольной трапеции вокруг её боковой стороны, перпендикулярной к основаниям. Получение усечённого конуса A B C D Усечённый конус получен вращением прямоугольной трапеции ABCD вокруг стороны CD.

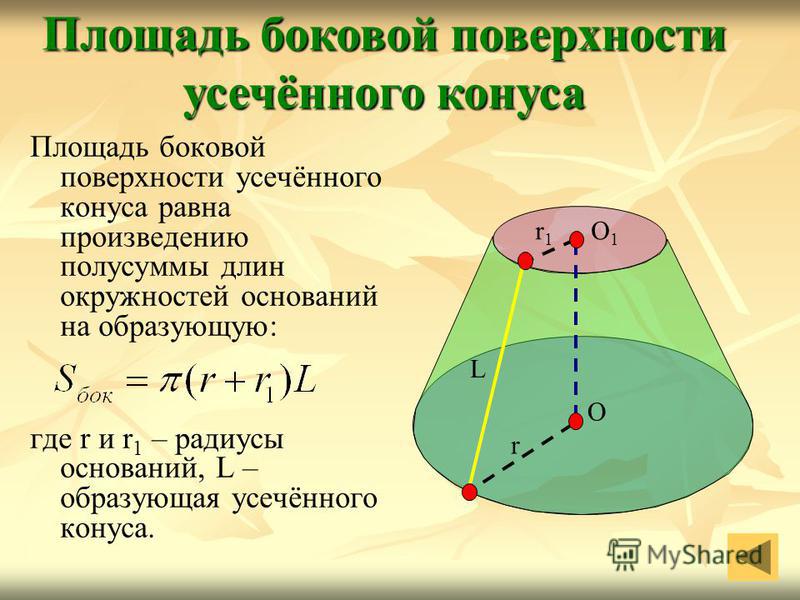
19

Площадь боковой поверхности усечённого конуса равна произведению полусуммы длин окружностей оснований на образующую: где r и r 1 – радиусы оснований, L – образующая усечённого конуса. Площадь боковой поверхности усечённого конуса О1О1 r1r1 r О L

Как сделать дымник – защиту для трубы?

Чтобы в дымовую трубу не попадали осадки, чтобы она не разрушалась льдом, её нужно защитить дымником. Мастера-жестянщики могут изготовить дымник на трубу самых причудливых форм, иногда на дымник устанавливают флюгер, указывающий направление ветра. Но сделать дымник простой конструкции на дымоходную трубу из металла или кирпича можно и своими руками.

Монтаж дымников

С давних времен дымники защищали дымоходы домов, не потеряли они своей актуальности и в наши дни. Если дровяные печи в домах сегодня редкость, то почти в каждом загородном доме есть камин, вытяжную трубу которого необходимо оградить от попадания в неё атмосферных осадков, птиц, осенней листвы и других посторонних предметов.

Нуждаются в такой же защите и все остальные трубы, выходящие на крышу: вентиляционные и дымовые трубы газовых отопительных приборов. Кроме защитной и декоративной функции, дымники способны выполнять ещё одну: они улучшают циркуляцию горячего воздуха в каминах и печах. Разберемся, как сделать дымник на трубу своими руками.

Виды дымников

Дымники могут отличаться друг от друга формой крыши, материалом изготовления, наличием дополнительных конструктивных элементов. Поэтому, прежде чем приступить к выполнению работ своими руками, стоит познакомиться с их разновидностями.

Формы крыши дымников

Достаточно внимательно посмотреть на крыши домов в какой-нибудь деревне или загородном поселке, чтобы убедиться в том, что человеческая фантазия неистощима на разные выдумки. Дымовые трубы украшают дымники самых разных форм, а некоторые умельцы приспосабливают вместо них дырявые чугунки, чайники, ведра и даже молочные фляги.

Если же вы хотите сделать настоящий красивый дымник своими руками, вам будет интересно узнать о том, какую форму ему можно придать. Различают следующие формы крыш дымников:

• Шатровая.
• Сводчатая (полуцилиндрическая).
• Двускатная.
• Четырехскатная (вальмовая).
• Четырехщипцовая.
• Шпилеобразная.
• Плоская и т. д.

На фотографиях ниже вы можете увидеть некоторые из перечисленных вариантов.

Дымник с вальмовой крышей

Дымник с четырехщипцовой крышей

Материалами для изготовления дымников чаще всего служат оцинкованная или нержавеющая сталь, листовая медь. Они могут иметь полимерное покрытие различных оттенков для защиты от коррозии.

Другие конусы, применяемые в машиностроении

Конусность 1:50 имеют установочные штифты, применяемые при необходимости дополнительного скрепления двух деталей, зафиксированных резьбовым соединением, чтобы они не могли перемещаться одна относительно другой. Установочные штифты вставляются в отверстия, просверленные и конически развернутые одновременно в обеих деталях, после их сборки. Конусность 1:50 соответствует углу уклона 0°34′.

Конус 1:16

Резьба обсадных труб 6 5/8″, бурильных и насосно-компрессорных труб, резьба трубная коническая общего назначения.

Конус 1:10

Концы валов электрических и других машин и соответствующие им муфты. ГОСТ 12081-72.

Центры упорные и конусы инструментов для тяжелых станков. ГОСТ 7343—72.

Отверстия под заклепки в котельных листах, мостовых и корабельных конструкциях (т. н. котельный конус).

Конус 1:1,866

Центры станков, центровые отверстия, потайные и полупотайные головки заклёпок диаметром 16—25 мм, потайные головки винтов диаметром 22—24 мм.

Что ещё можно сделать из бумажного конуса?

Бумажную заготовку для конуса можно использовать, чтобы сделать упаковку для сладкого подарка. Для этого на края, с внутренней стороны, добавляют кусочки двустороннего скотча, или же просто промазывают клеем.

Затем на эти участки помещаются листы гофрированной бумаги.

• Чтобы она красиво легла, нужно делать небольшие складки.
• После этого заготовка с бумагой склеивается в конус.
• Внутрь поделки помещаются конфеты или другие предметы, а гофрированный лист сверху завязывается ленточкой, образуя мешочек.
• На готовую упаковку можно добавить и другие декоративные элементы.

Бумажный конус можно использовать и для других поделок. Например, если делать его из плотного картона, то затем, с помощью ткани, получится создать вот такие игрушки животных или елочное украшение.

Роликовые вращатели самоцентрирующиеся INZT 10 E

Линейная скорость, мм/мин 100-1000 Диаметр заготовки, мм 500-3600 Размер роликов, мм 250х100

предлагает свои услуги по вальцовке металла с применением современного высокотехнологичного оборудования. Суть этой технологической операции состоит в холодном деформировании листовых материалов на специальных станках вдоль заданного направления. В процессе вальцевания листа металла он проходит или прокатывается между несколькими валами и происходит его подгибание до требуемого радиуса. Мы обеспечиваем комплексный подход к решению самых разных технических задач заказчика – любого уровня сложности и масштабов. Отличное оснащение производственной площадки, использование станков с ЧПУ и мастерство наших специалистов – все это служит гарантией успеха и высокого качества работ.

Усеченный геометрический объект

Усеченная фигура представляет собой объект в пространстве, который состоит из двух оснований разной площади и конической боковой поверхности. В отличие от исходного конуса, его усеченный вариант не имеет вершины. Остальные линейные элементы для него такие же, как для конуса с вершиной. У усеченной фигуры также имеется две директрисы, ограничивающие каждое из оснований, и одна генератриса, которая опирается на линии направляющих кривых.

Рассматриваемый геометрический объект также бывает нескольких видов (эллиптический, наклонный). Чаще всего в задачах по геометрии встречается именно круглый прямой усеченный конус, который ограничен двумя круглыми основаниями.

Способы построения

Можно выделить два основных способа построения усеченного круглого геометрического объекта:

• из круглого прямого конуса;
• с помощью трапеции.

В первом случае необходимо взять коническую фигуру и режущую плоскость, которая будет параллельна основанию. После этого с помощью плоскости следует отсечь верхнюю часть конуса. Оставшаяся под плоскостью фигура будет усеченной

Следует отметить, что совершенно неважно, какая часть конуса с вершиной будет отсечена. Чем больше она будет, тем ближе окажутся друг к другу значения верхнего и нижнего радиусов в усеченной фигуре, то есть тем ближе она по форме будет походить на прямой цилиндр.

Если прямоугольную трапецию поставить на большее основание и вращать ее вокруг перпендикуляра h, то получится усеченный конус. В нем отрезки a и b будут радиусами оснований объемной фигуры, перпендикуляр h станет высотой, а наклонный отрезок g будет представлять собой длину образующей. Эти четыре линейных характеристики определяют рассматриваемую объемную фигуру. Следует заметить, что для однозначного построения фигуры достаточно лишь трех любых из них, например, высоты и двух радиусов.

Площадь поверхности

Поверхность усеченной фигуры, в отличие от полного конуса, образована тремя частями: два круглых основания и боковая поверхность. Площади круглых оснований вычисляются по известной формуле для круга: pi*r2. Для боковой поверхности следует выполнить следующие действия:

Разрезать ее вдоль образующей и развернуть на плоскости.
Обратить внимание, что полученная фигура представляет собой сектор круга, у которого в верхней его части вырезан другой маленький сектор.
Достроить мысленно усеченную фигуру до полного конуса и определить его высоту H и директрису G. Через соответствующие параметры усеченного конуса они будут выражаться следующим образом: G = r1*g/(r1-r2), H = h*r1/(r1-r2), здесь радиусы оснований r1 и r2 такие, что r1>r2.
Рассчитать площади большого и маленького круговых секторов, а затем вычесть из первой вторую

В итоге получится следующая простая формула: Sb = pi*g*(r1 + r2).

Площадь всей поверхности рассматриваемой фигуры вычисляется как сумма трех величин S1, S2 и Sb:

S = S1 + S2 + Sb = pi*r12 + pi*r22 + pi*g*(r1 + r2).

Для определения величины S необходимо знать три линейных параметра усеченного конуса: радиусы оснований и длину генератрисы.

Формула объема

Для определения объема следует воспользоваться приемами, подобными тем, которые описаны в методике определения площади поверхности. Для начала следует усеченный конус достроить до полного, затем вычислить объемы фигур с высотами H и H-h по уже известной формуле. Разница этих объемов даст искомую формулу для усеченной фигуры с круглыми основаниями:

V = 1/3*pi*r12*H — 1/3*pi*r22*(H-h).

Подставляя в это выражение равенство для высоты H через линейные характеристики усеченной фигуры, можно получить конечную формулу:

V = 1/3*pi*h*(r12 + r22 + r1*r2).

Это выражение можно переписать не через линейные параметры, а через площади оснований фигуры S1 и S2:

V = 1/3*h*(S1 + S2 + (S1*S2)^0,5).

Записанная формула объема может быть получена универсальным способом без привлечения известного выражения для полного конуса. Для этого необходимо использовать интегральное исчисление, разбивая при этом усеченный геометрический объект на бесконечное количество тонких круглых дисков. Их радиусы будут постепенно уменьшаться от r1 до r2. Этот метод вывода формулы для объема не отличается от аналогичного для полного круглого конуса, изменяются лишь пределы интегрирования.