Площадь

Предремонтные замеры пола

Как рассчитать площадь пола перед проведением ремонтных работ, например, замены линолеума или покраски? Для квадратного или прямоугольного помещения сначала нужно будет измерить длину и ширину комнаты. Затем умножить длину и ширину, получим длина x ширина = площадь. Таким образом, если комната имеет размеры 3 метра в ширину и 5 метров в длину, общая площадь составит 15 квадратных метров.

Это измерение можно использовать при расчете необходимого количества плиточного раствора, герметика, линолеума, которые владелец планирует использовать для своего проекта. Чтобы рассчитать площадь для подбора материалов, как правило, нужно добавить 10% коэффициент запаса: просто умножьте площадь на 1,1, а затем округлите до целого значения.

В примере, когда общая площадь составляет 15 м2, нужно будет заказать дополнительное количество плитки и раствора для 16,5 квадратных метра. Если комната не прямоугольная, нужно разделить ее на две или более элементарных геометрических фигур, чтобы рассчитать общую площадь.

Треугольник

Треугольник — это когда три отрезка соединяют три точки, не лежащие на одной прямой. Эти три точки принято называть вершинами, а отрезки — сторонами. Рассчитать площадь треугольника можно несколькими способами по исходными данным, давайте их рассмотрим.

Если известна сторона и высота.

S = 0,5 * a * h, где a — длина основания, h — высота, проведенная к основанию.

Основание может быть расположено иначе, например так:

При тупом угле высоту можно отразить на продолжение основания:

При прямом угле основанием и высотой будут его катеты:

Если есть радиус вписанной окружности.

S = p * r, где р — полупериметр треугольника, r — радиус вписанной окружности.

У нас есть отличные онлайн занятия с лучшими преподавателями по математике! Для учеников с 1 по 11 классы!

Как рассчитать площадь стен в квадратных метрах?

Наш онлайн-калькулятор рассчитывает площадь стен в стандартной планировке по классическим математическим формулам определения площади простых фигур:

Sстен = (a× b)1 + .. + (a × b)4 — ((a × b)окна × n) — ((a × b)двери × n), где a, b – стороны, n – количество.

Если же в вашем случае, стены имеют нестандартную форму – треугольника, трапеции или неправильного четырехугольника (например, в мансардном помещении), рекомендуем самостоятельно воспользоваться соответствующими формулами расчета площади стен и выполнить операцию вручную. В более сложных ситуациях, необходимо разбивать поверхности на отдельные фигуры и складывать получившиеся значения.

• Формула расчета площади стен треугольной формы: S = (a × h) / 2, где а – основание, h – высота.
• Формула расчета площади стен квадратной формы: S = a 2 , где а – сторона.
• Формула расчета площади стен прямоугольной формы: S = a × b, где а, b – стороны.
• Формула расчета площади стен трапециевидной формы: S = ((a + b)× h)/ 2, где a, b – основания, h – высота.

Периодически нам требуется знать площадь и объем комнаты. Эти данные могут понадобиться при проектировании отопления и вентиляции, при закупке стройматериалов и еще во многих других ситуациях. Также периодически требуется знать площадь стен. Все эти данные вычисляются легко, но предварительно придется поработать рулеткой — измерять все требуемые габариты. О том, как посчитать площадь комнаты и стен, объем помещения и пойдет речь дальше.

Часто требуется посчитать кубатуру комнаты, ее объем

Простые геометрические фигуры крыш

Прежде чем выполнять кровельные работы, нужно знать, как рассчитать площадь крыши, чтобы определить, сколько материала потребуется. Его количество всегда нужно брать с запасом и добавлять не менее 10 процентов от общей площади кровли для учета отходов строительства.

Предварительно перед расчетом схему кровли разбивают на простые геометрические фигуры, в нашем примере это две трапеции и два треугольника. Как рассчитать площадь крыши для трапециевидных элементов? Площадь вычисляется по следующей формуле: S=(a+b)xh/2, где: а – ширина нижнего свеса — 10 м, b – ширина по коньку — 7 м, h – высота — 5 м.

Для треугольных элементов применяется формула: S=axh/2, где: а – ширина ската по нижнему свесу — 7 м, h – высота ската — 3 м.

Порядок измерения:

1. Измерить длину, ширину и высоту каждой геометрической фигуры крыши, включая ветровые окна. Эта информация может быть доступна в исходном плане здания дома или, если поверхность крыши относительно низкая и плоская, можно ее измерить самостоятельно. Если хозяин дома сам не может безопасно подняться на крышу, расчет можно выполнить по наружным замерам здания.
2. Перемножить длину и ширину каждой треугольной или трапецеидальной плоскости в отдельности.
3. Вычислить площадь для симметричных треугольных плоскостей, умножив длину основания треугольника (самую длинную сторону) на его высоту (расстояние от середины самой длинной стороны до противоположного угла).
4. Затем разделите итог на 2, чтобы получить результат в квадратных метрах. S=axh/2=7х3/2=10,5 м2.
5. Вычислить площадь для трапеции, умножив ширину нижнего свеса плюс ширину по коньку на его высоту (расстояние от середины самой длинной стороны до противоположного угла).
6. Затем разделить итог на 2, чтобы получить результат в квадратных метрах.
7. Умножить площадь на 0,1, чтобы получить 10-процентную надбавку для запаса кровельного материала S=(a+b)xh/2=(10+7)*5/2= 42,5 м2.
8. Сложить площади всех фигур вместе. S=10,5+10,5+42,5+42,5=106 м2.
9. В результате получается общая площадь крыши 106 м2, с запасом — 116 м2.

Как рассчитать площадь комнаты стандартной формы

Под площадью комнаты подразумеваются числовые характеристики, которые показывают её размер в двухмерном пространстве. Если комната стандартная (прямоугольная или квадратная), то сделать расчёт легко. Нужно только померить длину и ширину. Делается это вдоль стен по полу, при загроможденности данных участков, возможно, проводить замер посредине комнаты.

Важно, одна сторона должна измеряться строго перпендикулярно второй. Стороны расположенные параллельно должны иметь один размер, но несмотря на это, меряются обе

Кроме того, следует проверить правильность формы, то есть провести промеры диагоналей. В прямоугольном или квадратном помещении, они должны равняться, или иметь небольшие отклонения.

Квадратное помещение

Как рассчитать S квадратных помещений — это довольно легко. У квадратной комнаты все стороны равны.  Однако, как говорилось выше, надо замерить их все, и взять средне арифметический показатель для расчёта:

А — размер сторон.

Рассмотрим пример: комната со стенами по 3 метра, 3 в квадрате — S = 9 м2.

Прямоугольное

Рассчитать площадь помещений прямоугольной конфигурации, также легко путём следующих вычислений:

На примере видно, при ширине 4,10 м, длине 6,15 м, S комнаты получается — 4,10 x 6,15 = 25,215 м2. После запятой оставляется две цифры, остальные округляются, то есть выходит 25,22 м2.

Формулы параллелограмма

Параллелограмм является четырехсторонним многоугольником с двумя парами параллельных сторон одинаковой длины. По определению, прямоугольник также представляет собой тип параллелограмма, но с равными углами

Площадь параллелограмма вычисляется так же, как и для прямоугольника (высота × ширина), но важно понимать, что высота означает не длину вертикальных сторон, а расстояние между сторонами

Из рисунка видно, что высота — это расстояние между двумя параллельными сторонами параллелограмма, расположенная под прямым углом между ними. S=ADxh. S=bxh, где AD=b — основание, h — высота.

Пример. Если параллелограмм имеет основание 3 см, а высоту 2 см, то площадь S равна произведению основания на высоту. Следовательно, имеем: S=3х2=6.

Ответ: 6 см2.

Информация о прямоугольнике

Прямоугольник — четырехугольная геометрическая фигура, противолежащие стороны которой равны и углы являются прямыми. Частным случаем данной фигуры считается квадрат. У него все углы прямые, а также все стороны равны между собой. Для выполнения расчетов нужно знать основные соотношения, свойства и признаки.

Важным аспектом является идентификация фигуры и применение к ней формул и соотношений. В двухмерной геометрии, которую еще называют эвклидовой, можно встретить необычный признак, позволяющий определить принадлежность четырехугольника к прямоугольнику. Его формулировка следующая: достаточно хотя бы трех углов, равных 90 градусам, чтобы четырехугольник считался прямоугольником.

Утверждение легко доказывается. Это связано с тем, что по теореме о сумме внутренних углов произвольного четырехугольника, составляющей 360 градусов, четвертый угол тоже равен 90. Нужно выполнить следующие расчеты для определения градусной меры четвертого угла: D = 360 — (90 + 90 + 90) = 90. Необходимо отметить, что смежные с ними углы равны 90.

Свойства и признаки

Очень часто новички путают свойства и признаки фигуры. Однако это совсем различные понятия. Признаками фигуры называются характерные особенности, которые позволяют отнести ее к тому или иному классу. Свойства — совокупность аксиом, позволяющих использовать некоторые данные при решении или доказательстве теорем и тождеств. Прямоугольник обладает следующими признаками:

1. Условие параллельности и равенства противоположных сторон.
2. Наличие четырех прямых углов.
3. Равенство диагоналей.
4. Квадрат диагонали равен суммарному значению квадратов двух сторон, которые не противоположны.
5. Все стороны не равны между собой.

Очень важно уметь различать геометрические фигуры. Поскольку прямоугольник является параллелограммом, то их часто путают

Основное его отличие — это равенство всех углов 90 градусов. У параллелограмма и ромба углы будут равняться 90 в том случае, когда они являются квадратами. Последний отличается от искомой фигуры (прямоугольника) равенством всех сторон. Поскольку прямоугольник является частным случаем параллелограмма, то обладает такими же свойствами:

1. Углы равны между собой 90 градусов.
2. Противолежащие параллельные стороны равны.
3. Сумма всех внутренних углов составляет 360.
4. Диагональ, проведенная внутри прямоугольника, делит его на два равнозначных треугольника, которые являются равновеликими. Они равны по третьему признаку равенства треугольников (размерности сторон одной фигуры равны значениям сторон другой фигуры).
5. Треугольники, полученные при проведении двух диагоналей, равны по всем признакам (углам и сторонам).
6. Диагонали пересекаются между собой в точке, которая делит их на четыре равные части.
7. Точка пересечения диагоналей — центр симметрии.
8. Сумма квадратов двух диагоналей соответствует суммарному значению квадратов всех сторон фигуры.

Периметр и размерность

Нужно ввести некоторые обозначения. Пусть стороны прямоугольника АВСД обозначаются литерами a и b. Поскольку диагонали равны, то можно только обозначить размерность одной буквой «d». Периметром называется сумма всех сторон заданной фигуры. Он обозначается литерой P. Для его нахождения применяется формула такого вида: P = 2 * (a + b). Однако бывает случай, когда известна только одна его сторона и диагональ. Формула приобретает следующий вид: P = 2a + ^(1/2) и P = 2b + ^(1/2).

Чтобы вычислить площадь прямоугольника, следует воспользоваться таким соотношением: S = a * b. Эта базовая формула, которая используется также в строительной сфере и физике. Однако существует еще один способ, с помощью которого можно узнать площадь прямоугольника. Она находится с помощью формулы Герона для треугольников с площадями S1 и S2, а затем результат умножается на 2. Эта особенность основывается на свойстве фигуры, поскольку диагональ делит его на два равных треугольника.

Соотношение имеет следующий вид: S = S1 + S2 = 2S1= 2 * ^(1/2). Переменная «p» — полупериметр треугольника. Он находится таким методом: p = P / 2 = (a + b + d) / 2.

Как посчитать площадь стен

Чтобы определить площадь стен, нужно знать, как рассчитать периметр комнаты. Определение площади часто требуется для закупки всевозможных материалов для отделки. Кроме длины и ширины помещения, понадобится выяснить высоту комнаты, а также габариты проемов двери и окон.

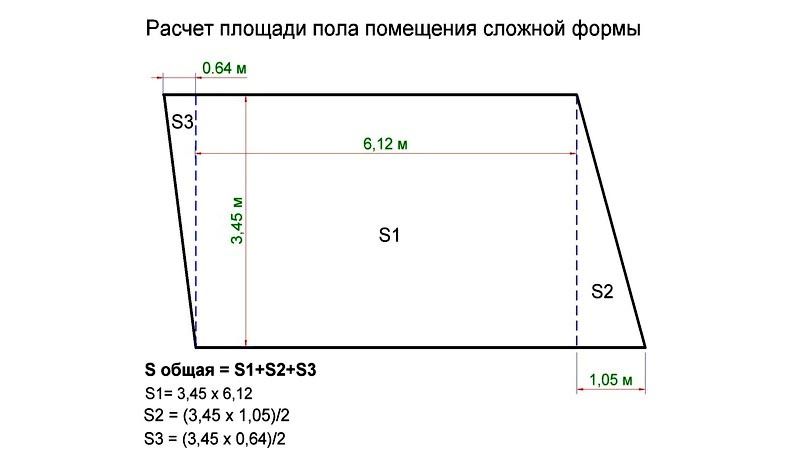Расчет площади стен сложной конфигурации

При расчетах стоит учитывать, что высота потолков даже в одном помещении может варьироваться, особенно если комната мансардного типа. Отдельно вычисляются значения всех стен, а затем их них отнимаются оконные и дверные проемы.

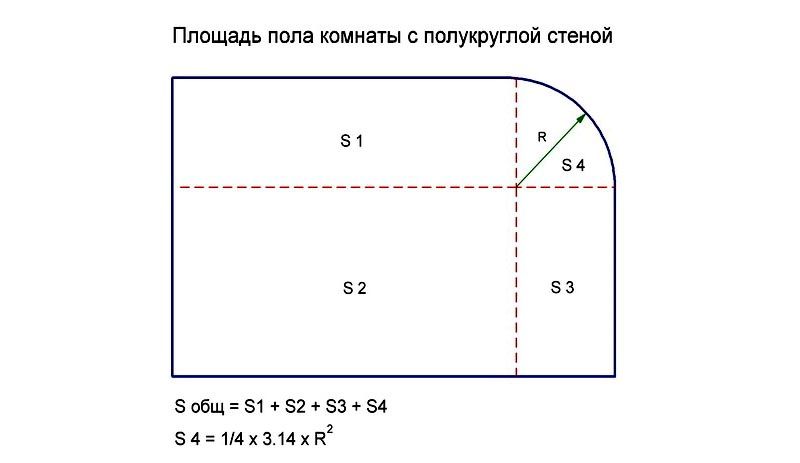Вычисления при полукруглой стене

Точные значения можно выявить с помощью калькулятора расчета площади стен комнаты. Иногда требуется определить объем помещения. В такой ситуации необходимо перемножить три значения: длину, ширину и высоту комнаты. Данный показатель меряется в кубических метрах.

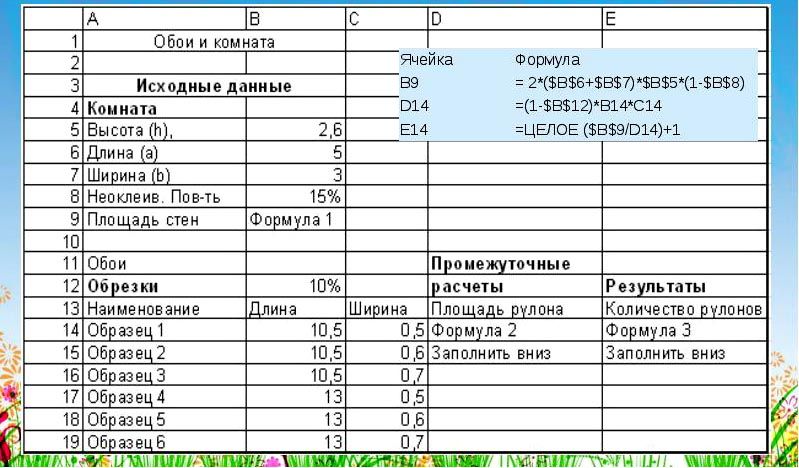Пример расчета обоев с помощью специальной электронной программки

Если помещение имеет разноуровневое зонирование, то можно провести такие расчеты:

• померить все участки стен. Замеры рекомендуется выполнять поближе к потолку;
• вычислить показатели площади по полу;
• на каждом вертикальном участке необходимо промерить длину и высоту, а затем данные значения перемножить;
• прибавьте показатели к значению пола.

У каждой комнаты есть оптимальные параметры, которые можно учитывать при планировке строительного объекта. Минимальный показатель жилого помещения равняется 8 кв. м. Комната общего назначения, такая как зал или гостиная может иметь площадь от 14 до 25 кв. м. Минимальный показатель высоты помещения составляет 240 см. Если потолок более трех метров, то такое пространство сложнее обогревать. Кухня должна иметь площадь не менее 6 кв. м.

Проведение грамотных расчетов позволит создать уютный интерьер даже при сложной конструкции

Правильное вычисление площади помещения является гарантией качественного проведения ремонта. Такой подход позволит свести к минимуму затраты на приобретение материалов.

Как посчитать площадь стен можно посмотреть на видео:

Watch this video on YouTube

Предыдущая РемонтКрасивые и практичные перегородки для зонирования пространства в комнате: 70 идей и советы дизайнеров
Следующая РемонтКак сделать клейстер: технологии и особенности применения

Площадь комнаты в квадратных метрах

Рассчитать его несложно, нужно просто запомнить простейшие формулы, а также произвести замеры. Для этого вам понадобятся:

• Рулетка. Лучше — с пряжкой, но уместно и обыкновенно.
• Бумага и карандаш или ручка.
• Калькулятор (или счет в столбик или в уме).

Набор инструментов неприхотлив, его можно найти в любом доме. С помощником делать замеры проще, но можно и самому.

Для начала необходимо измерить длину стен. Желательно делать это вдоль стен, но если все они загружены тяжелой мебелью, можно измерить и внутри. Только в этом случае необходимо следить, чтобы рулетка лежала вдоль стен, а не наискось — погрешность измерения будет меньше.

Прямоугольная комната

Если комната имеет правильную форму и не имеет выступающих частей, рассчитать площадь комнаты несложно. Измерьте длину и ширину и запишите их на листе бумаги. Введите числа в метрах, а затем вставьте сантиметры после десятичной точки. Например, длина составляет 4,35 м (430 см), а ширина — 3,25 м (325 см).

Как рассчитать площадь комнаты

Умножаем найденные числа, получаем площадь комнаты в квадратных метрах. Если вернуться к нашему примеру, мы получим следующую информацию: 4,35 м * 3,25 м = 14,1375 квадратных метров. В этом значении обычно оставляют две цифры после десятичной точки, поэтому округлите их в большую сторону. Итак, расчетная площадь помещения составляет 14,14 квадратных метра.

Помещение неправильной формы

Если нужно рассчитать площадь комнаты неправильной формы, ее делят на простые формы — квадраты, прямоугольники, треугольники. Затем измерьте все необходимые размеры и произведите расчеты.

Перед тем, как рассчитать площадь комнаты, тоже вносим изменения. Только в этом случае цифр будет не два, а четыре: прибавьте выступу длину и ширину. Размеры обоих элементов считаются отдельно.

Один из примеров — на фото. Поскольку оба они прямоугольные, площадь рассчитывается по той же формуле: длина умножается на ширину. Найденное число следует вычесть или прибавить к размеру комнаты — в зависимости от конфигурации.

Площадь помещения сложной формы

Воспользуемся этим примером, чтобы рассчитать площадь комнаты с выступом:

1. Рассчитайте площадь без свеса: 3,6 м * 8,5 м = 30,6 кв.
2. Рассчитываем размеры выступающей части: 3,25 м * 0,8 м = 2,6 м2.
3. Сложите эти два значения: 30,6 м2 + 2,6 м2. = 33,2 м2.

Есть и комнаты со скошенными стенами. В этом случае разделите его так, чтобы у вас получились прямоугольники и треугольники (как на картинке ниже). Как видите, в этом случае требуется пять измерений. Деление можно было сделать иначе, поставив вертикальную линию, а не горизонтальную

Это не важно. Для этого требуется только набор простых форм, и вы можете выбирать их бесплатно

Как рассчитать площадь комнаты неправильной формы?

В этом случае порядок расчета следующий:

1. Считаем большую прямоугольную часть: 6,4 м * 1,4 м = 8,96 кв. После округления получаем 9,0 м2.
2. Рассчитываем небольшой прямоугольник: 2,7 м * 1,9 м = 5,13 кв м. После округления получаем 5,1 м2.
3. Найдите площадь этого треугольника. Поскольку он имеет прямой угол, его площадь составляет половину площади прямоугольника с такими же размерами. (1,3 м * 1,9 м) / 2 = 1,235 м². После округления получаем 1,2 кв.
4. Теперь сложите, чтобы найти общую площадь комнаты: 9,0 + 5,1 + 1,2 = 15,3 квадратных метра.

Планировка комнат может быть самой разнообразной, но вы понимаете общее правило: разделитесь на простые формы, отмерьте все необходимые размеры, посчитайте площадь каждого фрагмента, а затем все просуммируйте.

Формулы для расчета площади и периметра простых геометрических фигур

Еще одно важное замечание: площадь комнаты, пола и потолка — одинаковые значения. Возможны отличия в случае с полуколоннами, не доходящими до потолка

Затем площадь этих элементов вычитается из общей площади. Результат — площадь пола.

Как подготовиться к расчетам

Проведение подготовительных манипуляций заключается в подготовке места для измерений. Также необходимо подготовить инструмент и специальные принадлежности. Лучше если комната будет свободной от посторонних предметов. Часто такое случается при замерах в новом доме или во время проведения ремонта. Замеры длины сторон производятся вдоль стенок. При этом нужно освободить хотя-бы участки, для свободного проведения рулеткой. Результаты замеров можно сразу же перенести на схему. Обязательно следует проверить прямоугольности комнаты. Для этого выполняется замер диагональных линий.

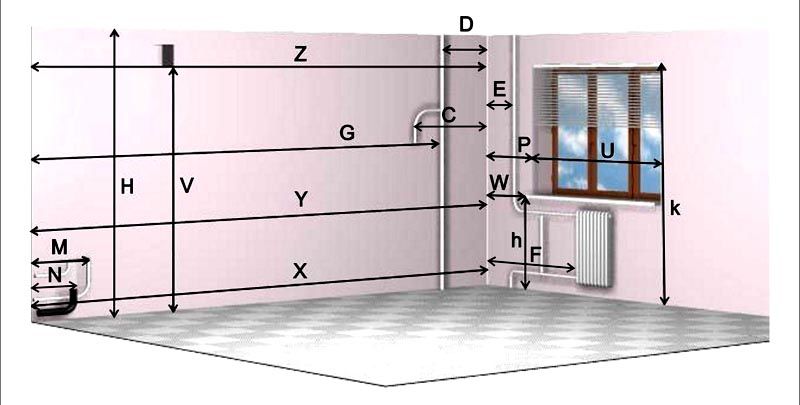Особенности замеров с учетом линий коммуникаций

Кроме рулетки вам может понадобиться специальная линейка для проверки прямых линий. Это может быть строительный уровень или правило. Иногда необходим строительный угольник больших размеров. Как вариант, самодельный циркуль. Можно использовать кусок шнура, привязанный к острому штырю. Для пола можно использовать специальные принадлежности для замеров. Для этого подойдет маркер, мел или скотч. Замеры выполняйте несколько раз. Это позволит избежать ошибки. Следите, чтобы лента для проведения замеров не провисала. Помните, что на многие измерительные инструменты наносится две шкалы. Нельзя путать метрическую систему и дюймовую.

Лазерное приспособление заметно облегчает работу

Перед замерами набросайте простой план – схему на бумаге. Это позволит правильно распределить все замеры. Стоит учитывать, что многие формулы расчетов очень сложные. В этом случае посчитать в столбик не получится. Чтобы посчитать без ошибок, можно воспользоваться программой Excel.

На схеме показаны все необходимые замеры для правильных расчетов

Немного теории

Как найти площадь различных фигур, проходили еще в начальной школе. Было это давно, так что «обновить» информацию может быть полезно. Будем рассматривать только то, что может иметь отношение к полу. Итак, начнем с самого простого — единиц измерения.

Чтобы посчитать площадь комнаты в квадратных метрах, нужен будет карандаш, рулетка и некоторый багаж знаний

Что такое 1 см² и 1 м²

Площадь любой фигуры измеряется в квадратных метрах или в квадратных сантиметрах. Обозначение см² или м², может встречаться написание кв.м, кв. см., кв. метры, кв. сантиметры и другие вариации.

Что такое один квадратный сантиметр

Один квадратный сантиметр — это площадь квадрата со стороной 1 см. Если нарисовать такой квадрат, стороны которого равны 1 см, то заштрихованная часть (на рисунке красным или синим) и будет один квадратный сантиметр. Соответственно, квадрат со стороной один метр — 1 м — имеет площадь один квадратный метр. Тот самый «квадрат площади». То есть, это квадратный участок пола (или стены) со стороной в один метр — 1 м².  В одном квадратном метре десять тысяч квадратных сантиметров: 1 м² = 10000 см².

Формулы

Это то, что касалось единиц измерения и их соответствия. Но наши помещения, слава богу, больше чем один квадратный метр. Как посчитать площадь комнаты? Сколько в ней квадратных метров? Обычно комната имеет форму прямоугольника, реже — квадрата. Значит, надо будет вспомнить формулы нахождения площади квадрата и прямоугольника.

При помощи очень простых формул, можно рассчитать площадь прямоугольника и квадрата

Надо длины сторон прямоугольника перемножить. Получим искомую площадь. Давайте потренируемся.

1. Имеем прямоугольник со сторонами 80 см и 50 см. Перемножаем эти цифры: 80 * 50 = 4000 см². Это и будет его площадь.
2. Стороны 322 см и 300 см. Получим: 322*300 = 96000 см².
3. Есть квадрат со стороной 60 см. Его площадь — 60 * 60 = 3600 см².

В случае с квадратом длину стороны можно возвести в квадрат — получится одно и то же. Но можно не морочить голову. Проще помнить, что надо стороны умножить.

Простейший калкулятор для расчета площади прямоугольной комнаты.

Перевод квадратных сантиметров в квадратные метры

Когда имеем дело с сотнями сантиметров, удобнее и проще считать в метрах. Мы знаем, что в одном метре сто сантиметров. Давайте решим те же примеры, но переведем сантиметры в метры:

1. 80 см = 0,8 м; 50 см = 0,5 м. Перемножаем 0,8*0,5 = 0,4 м². То есть, 0,4 квадратных метра.
2. 322 см это 3,22 м; 300 см это 3 м. Теперь умножаем полученные цифры: 3,22 * 3 = 9,6 м².
3. 60 см равны 0,6 м. Площадь квадрата с такой стороной 0,6*0,6 = 0,36 м².

Цифры получаются намного меньше, запомнить их проще. И если мы хотим посчитать площадь комнаты в квадратных метрах, ее размеры мы меряем в метрах, а не сантиметрах. Можно перевести квадратные сантиметры в квадратные метры. Как уже говорили, в одном квадратном метре содержится десять тысяч квадратных сантиметров.

Соотношение квадратных сантиметров и квадратных метров

Если же у вас есть площадь в квадратных сантиметрах, чтобы перевести ее в квадратные метры, цифру надо разделить на 10 000. Например:

• 4000 см² / 10000 = 0,4 м²;
• 96000 см² / 10000 = 9,6 м²;
• 3600 см²/ 10000 = 0,36 м².

Как видите, все просто. Надо только запомнить основные положения и посчитать площадь комнаты в квадратных метрах будет совсем несложно. Нужно будет предварительно провести измерения, а потом заняться расчетами.

Формулы расчета

Зная площади простых фигур, можно находить параметры более сложных. Античными математиками были выведены формулы, по которым можно легко их вычислять. Такими фигурами являются треугольник, четырёхугольник, многоугольник, круг.

Чтобы найти площадь сложной плоской фигуры, её разбивают на множество простых фигур, таких как треугольники, трапеции или прямоугольники. Затем математическими методами выводят формулу для площади этой фигуры. Подобный метод используют не только в геометрии, но и в математическом анализе для вычисления площадей фигур, ограниченных кривыми.

Треугольник

Начнём с самой простой фигуры — треугольника. Они бывают прямоугольные, равнобедренные и равносторонние. Возьмём любой треугольник ABC со сторонами AB=a, BC=b и AC=c (∆ ABC). Чтобы найти его площадь, вспомним известные из школьного курса математики теоремы синусов и косинусов. Отпуская все выкладки, придём к следующим формулам:

• S=√ — известная всем формула Герона, где p=(a+b+c)/2 — полупериметр треугольника;
• S=a•h/2, где h — высота, опущенная на сторону a;
• S=a•b•(sin γ)/2, где γ — угол между сторонами a и b;
• S=a•b/2, если ∆ ABC — прямоугольный (здесь a и b — катеты);
• S=b²•(sin (2•β))/2, если ∆ ABC — равнобедренный (здесь b — одно из «бёдер», β — угол между «бёдрами» треугольника);
• S=a²•√¾, если ∆ ABC — равносторонний (здесь a — сторона треугольника).

Четырёхугольник

Пусть имеется четырёхугольник ABCD, у которого AB=a, BC=b, CD=c, AD=d. Чтобы найти площадь S произвольного 4-угольника, нужно разделить его диагональю на два треугольника, площади которых S1 и S2 в общем случае не равны.

Затем по формулам вычислить их и сложить, т. е. S=S1+S2. Однако, если 4-угольник принадлежит к определённому классу, то его площадь можно найти по заранее известным формулам:

• S=(a+c)•h/2=e•h, если 4-угольник — трапеция (здесь a и c — основания, e — средняя линия трапеции, h — высота, опущенная на одно из оснований трапеции;
• S=a•h=a•b•sin φ=d1•d2•(sin φ)/2, если ABCD — параллелограмм (здесь φ — угол между сторонами a и b, h — высота, опущенная на сторону a, d1 и d2 — диагонали);
• S=a•b=d²/2, если ABCD — прямоугольник (d — диагональ);
• S=a²•sin φ=P²•(sin φ)/16=d1•d2/2, если ABCD — ромб (a — сторона ромба, φ — один из его углов, P — периметр);
• S=a²=P²/16=d²/2, если ABCD — квадрат.

Многоугольник

Чтобы найти площадь n-угольника, математики разбивают его на простейшие равные фигуры —треугольники, находят площадь каждого из них и затем складывают. Но если многоугольник относится к классу правильных, то используют формулу:

S=a•n•h/2=a²•n/[4•tg (180°/n)]=P²/[4•n•tg (180°/n)], где n — количество вершин (или сторон) многоугольника, a — сторона n-угольника, P — его периметр, h — апофема, т. е. отрезок, проведённый из центра многоугольника к одной из его сторон под углом 90°.

Круг — это совершенный многоугольник, имеющий бесконечное число сторон. Нам необходимо вычислить предел выражения справа в формуле площади многоугольника при числе сторон n, стремящемуся к бесконечности. В этом случае периметр многоугольника превратится в длину окружности радиуса R, которая будет границей нашего круга, и станет равен P=2•π•R. Подставим это выражение в указанную выше формулу. Мы получим:

Найдём предел этого выражения при n→∞. Чтобы это сделать, учтём, что lim (cos (180°/n)) при n→∞ равен cos 0°=1 (lim — знак предела), а lim [1/(n•sin (180°/n))]= lim [1/(n•sin (π/n))] при n→∞ равен 1/π (мы перевели градусную меру в радианную, используя соотношение π рад=180°, и применили первый замечательный предел lim (sin x)/x=1 при x→∞). Подставив в последнее выражение для S полученные значения, придём к известной формуле:

Простой расчет прямоугольника

Если внимательно посмотреть вокруг, можно увидеть множество примеров прямоугольников. По определению, прямоугольник представляет собой четырехсторонний многоугольник, углы которой находятся под прямым углом, равным 90 градусам. Рассчитать площадь поверхности тела прямоугольника — простая математическая операция, которая наиболее часто применяется человеком в повседневной жизни

Почему важно знать формулу площади? Многие предметы и обстановка, окружающие человека, имеют прямоугольную форму: дом, стены, пол, крыша. И очень часто надо знать их площадь для строительства или ремонта

Если прямоугольник имеет длину b и ширину h, мы можем найти площадь S, умножив ширину на его длину. Следовательно: S=bxh.

Пример. Как рассчитать площадь прямоугольника, если известны сторона и ширина, например, длина 4 см и ширина 3 см, тогда: S=4х3=12.

Ответ: 12 см2.

Квадрат — разновидность прямоугольника с равными углами и сторонами.

S=bxb=b2.

Пример. Если квадрат имеет стороны 3 см, мы можем найти S, возведя в квадрат значение стороны. Следовательно, имеем: S=3х3=9.

Ответ: 9 см2.

Виды треугольников

Треугольник представляет собой многоугольник, который имеет три стороны и может быть отнесен к следующим типам:

• Равносторонний треугольник имеет равные стороны и равные углы.
• Равнобедренный треугольник имеет две равные стороны и два равных угла.
• Разносторонний треугольник имеет три неравные стороны и три неравных угла.
• Прямоугольный треугольник имеет один прямой угол 90 градусов.
• Остроугольный треугольник имеет все углы меньше 90 градусов.
• Тупоугольный треугольник имеет один угол больше 90 градусов.

Площадь любого треугольника определяется по формулам.

1. Как рассчитать площадь треугольника, если известны высота и основание треугольника:

• S=1⁄2×a×h, где: h – высота, a — основание.
• S=1⁄2xa×b×sinα, где: a, b – любые две стороны, α — угол между ними.
• S=p×r, где: p = (a+b+c) / 2 — полупериметр, a, b, c – три стороны, r – радиус круга.

Площадь равностороннего треугольника:

S=a2х√3 ⁄4 , где a=b= c.

Площадь равнобедренного треугольника:

S=1⁄4xbx√(4a2-b2).

2. Как рассчитать площадь треугольника, если заданы две стороны и угол между ними:

S=1⁄2xaxbxsinC=1⁄2xbxcxsinA =1⁄2xaxcxsinB.

Пример 1: Найти S треугольника, сторона которого составляет 14 см, а высота — 10 см.

Решение: b=14 см, h=10 см, A=1⁄2х14х10=70

Ответ: 70 см2.

Пример 2. Найти область треугольника, стороны которого и угол между ними заданы следующим образом: a=5 см и b=7 см, C=45 градусов.

Решение: Площадь треугольника =1⁄2xaxbxsin 45.

Площадь =1⁄2×5×7×0,707 (поскольку sin45=0,707)

Площадь =1⁄2×24,745=12,3725

Ответ: 12,3725 см2.

Пример 3. Найдите площадь (в м2) равнобедренного треугольника, стороны которого составляют 10 м, а основание — 12 м.

Решение: Площадь равнобедренного треугольника определяется:

A=1⁄4xbx√(4a2-b2)A=1⁄4х12х√(4х(10)2-(12)2)А=48

Ответ: 48 м2.

Пример 4. Найти площадь треугольника, стороны которого равны 8, 9 и 11 соответственно. Все единицы измерения даны в метрах (м).

Решение: Стороны a=8, b=9 и c=11. Согласно формуле Херона площадь треугольника может быть определена по следующей формуле: A=√(sx(sa)х(sb)х(sc)). Прежде всего нам нужно определить s, которая является полупериметром треугольника: s =1⁄2х(a+b+c)=1⁄2х(8+9+11)=14.

Теперь, вставив значение полупериметра в формулу Герона, можно определить площадь треугольника: A=√(sx(sa)х(sb)х(sc)). A=√(14х(14-8)х(14-9)х(14-11)). A=√(1260)=35,50

Ответ: 35,50 м2.

Как квадратные метры перевести в погонные и просто в метры?

Правильный ответ — Нет, потому что квадратные метры и линейные метры являются единицами измерения разных категорий. Квадратные метры измеряют площадь, а погонные метры измеряют только длину изделия.

Вот краткое изложение терминов: квадратный метр и погонный метр.

Квадратный метр (кв.м; м2) в Международной системе единиц (СИ) — это площадь квадрата со стороной, равной 1 метру. Квадратный метр — это мера площади стен, полов, недвижимости, где площадь, например, офиса или квартиры равна площади пола. Или, если вам нужно посчитать количество керамической плитки на стене или линолеума на полу, вам нужно умножить длину на высоту и получить площадь в квадратных метрах. Хотя сам линолеум продается погонными метрами, но об этом ниже.

Обозначения в квадратных метрах (m2) используются в …

• Обмер зданий, домов, квартир, комнат;
• Замер облицовочных и террасных материалов;
• Измерение настила крыш и полов;
• Измерение площади, занимаемой оборудованием, мебелью

Концепция квадратных метров

Перевести квадратные метры в погонные метры, а просто в метры — НЕТ!

Один метр (рулон ткани, изделие, забор, мебель) — это длина вне зависимости от ширины. Так как цена материала входит в стоимость 1 погонного метра вагонки, линолеума или куба. Погонный метр линолеума шириной 3 метра будет, конечно, дороже линолеума шириной 2,5 метра.

Иногда погонные метры используются и при изготовлении кухонной мебели для удобных расчетов. Например, производитель подсчитал, что кухонный шкаф длиной 3 метра и шириной 60 сантиметров с необходимым количеством полок, ящиков, дверок будет стоить 1200 долларов по курсу Нацбанка. А как известно, кухня в наших квартирах разная, в основном небольшая, поэтому производитель ставит цену за 1 погонный метр в 400 долларов. Клиент может уместить только 2,5 метра. Обсуждаем стандартное оборудование, размещение полок, ящиков и вывозим цену 1000 долларов.

Подробнее: Как сделать высокие грядки своими руками

400 долларов США x 2,5 млн = 1000 долларов США

Обозначения в погонных метрах используются для измерения:

• Полы в рулонах (ткань в рулонах, ковролин, линолеум …);
• Доски, рейки, блок-хаус, плинтусы, иногда трубы, фитинги;
• Стоимость от цены мебели (кухни) со стандартной техникой и фурнитурой.