Площадь треугольника онлайн

Площадь равностороннего треугольника по стороне

Пусть в равносторннем треугольнике известна сторона a (a=b=c) (Рис.1):

Найдем площадь треугольника. Поскольку в треугольнике напротив равных сторон расположенные равные углы (см. статью Соотношения между сторонами и углами треугольника), то в равносторннем треугольнике все углы равны. Но сумма всех углов треугольника равна 180°. Следовательно все три угла равностороннего треугольника равны 60°. Для треугольника ABH применим теорему синусов:

Учитывая, что , получим:

Площадь треугольника по основанию и высоте имеет следующий вид:

Подставляя (1) в (2), получим:

Пример 1. Сторона равностороннего треугольника равна a=5. Найти площадь треугольника.

Решение. Для вычисления площади треугольника воспользуемся формулой (3). Подставляя значение a=5 в (3), получим:

Ответ:

Площадь прямоугольного треугольника по формуле Герона

Полупериметр: 

Сторона a
Сторона b
Сторона c

Для вычисления площади треугольника применяются различные формулы, в зависимости от известных исходных данных. Выше приведены формулы и калькулятор, который поможет вычислить площадь треугольника или проверить уже выполненные вычисления. Приведены общие формулы для всех типов треугольников, частные случаи для равносторонних, равнобедренных и прямоугольных треугольников.

Наш калькулятор для вычисления площади поможет вам вычислить площадь разных видов треугольников или проверить уже выполненные вычисления.

В зависимости от вида треугольника и его известных исходных данных, площадь треугольника можно вычислить по различным формулам.

Как рассчитать площадь комнаты пошаговая инструкция

При расчете площади нужно знать длину, ширину и высоту комнаты

Можно, конечно, заглянуть в техническую документацию дома и посмотреть в ней все нужные характеристики. Но, во-первых, там нередко бывают ошибки, во-вторых, иногда проще вычислить всё самостоятельно, чем найти документы.

Для проведения подсчётов нам понадобятся определённые инструменты, большинство из которых можно запросто найти в каждом доме. А именно:

• рулетка;
• карандаш;
• бумага для записей;
• калькулятор (можно использовать калькулятор, который размещён на нашем сайте);
• трезвость ума и ясность мыслей.

Пол

Чтобы высчитать квадратуру пола в прямоугольной или квадратной комнате, необходимо узнать её длину и ширину.

Проводить замеры лучше у основания стен, а для этого желательно отодвинуть или вынести всю мебель. Но, если такая процедура в ваши планы не входила, можно мерить и по центру. Главное при этом, чтобы воображаемая линия, по которой будет производиться измерение, располагалась под углом в 90° к стене.

После того как данные замеров получены и проверены, их нужно перемножить по формуле , где S — площадь в квадратных метрах, a и b — длина и ширина, соответственно.

Если к основному помещению прилегает ниша или какое-нибудь другое — его площадь необходимо вычислить по тому же алгоритму, и результаты приплюсовать к площади комнаты. Если есть различные выступы, которые занимают его часть — их также следует измерить и полученный результат вычесть из общего.

С квадратами и прямоугольниками всё просто. А как посчитать S комнаты, если она имеет неправильную форму? Здесь придётся применить логическое мышление, и немного вспомнить школьный курс алгебры и геометрии. Но давайте по порядку.

Если помещение неправильной формы

Постарайтесь мысленно или на бумаге разделить комнату на простые элементы (квадраты, прямоугольники, треугольники). Далее, нужно будет высчитать размеры каждого из них, и результаты сложить.

• для треугольника — . Где a — длинна основания треугольника, b — высота, проведённая от вершины к основанию;
• для круга — . Где 3,14, r — радиус круга (чтобы узнать радиус — найдите с помощью рулетки самое длинное расстояние между стенами и разделите его на 2);
• для полукруга — (буквенные обозначения совпадают с предыдущим пунктом).

Как оказалось, и в таком случае ничего сложного нет. Главное, тщательно проверять результаты замеров, чтобы в расчёты не закралась случайная ошибка, и их не пришлось производить заново.

И ещё. Если вы хотите произвести монтаж тёплого пола, не забудьте отдельно вычислить площадь, которую занимает мебель, и вычтите её из общего значения для помещения.

С полом мы разобрались. Но при подготовке, допустим, к переклеиванию обоев это вам мало чем поможет. Нужно будет узнать точное количество квадратных метров, которое занимают  стены.

Стены

Площадь каждой отдельно взятой стены можно высчитать так же, как и квадратуру пола. Только теперь вместо ширины помещения нужно будет измерить её высоту. Множим длину стены на высоту и получаем необходимый нам результат в квадратных метрах.

Измерение высоты лазерной рулеткой

А можно вычислить и для всех стен сразу. Для этого вам понадобится узнать периметр пространства. Возьмите рулетку и измерьте длину каждой стены, результаты сложите — это и будет периметр. Остаётся измерить высоту комнаты и воспользоваться следующей формулой: , где p — периметр, а h — высота.

Теперь необходимо разобраться с оконными, дверными и прочими проёмами, присутствующими в помещении.

Точнее, рассчитать площадь каждого из них (по формулам, представленным выше, в зависимости от формы проёма), результаты суммировать и вычесть из общего количества.

Существует также ряд общих рекомендаций по проведению замеров.

Формулы площади треугольника

Ⅰ. Через высоту и основание

\

Самая известная формула площади треугольника.
Зная только высоту и сторону, на которую падает
эта высота, можно найти площадь треугольника.

Ⅱ. Через все стороны и периметр

\

p — полупериметр, вычисляется по формуле: ​\( p = \frac{a+b+c}{2} \)​,a, b, c — стороны треугольника.

Это формулу, нужно использовать когда известны
все три стороны треугольника. Зная три стороны
треугольника можно найти периметр, а дальше
найти и площадь заданного треугольника.

Эту формулу площади также называют формулой Герона.

Ⅲ. Через две стороны и угол между ними

\

a, b — стороны между которыми расположен угол β,sin β — синус угла β.

Формула применяется, когда известен
один из углов, и две стороны, образующие
этот угол. В некоторых задачах площадь
треугольника можно найти только по этой формуле.

Ⅳ. Через периметр и радиус вписанной окружности

\

r — радиус вписанной окружности,
P — периметр треугольника.

Тут даже не обязательно знать все стороны треугольника,
достаточно знать периметр и радиус описанной окружности.

Ⅴ. Через все стороны и радиус описанной окружности

\

abc — произведение всех сторон треугольника,R — радиус описанной окружности.

Пожалуй, единственная формула, где площадь
треугольника можно найти только через радиус
описанной окружности и произведение трех сторон.

Ⅵ. Через сторону и два прилежащих к ней угла

\

a — сторона треугольника,sin α — синус угла α,sin β — синус угла β.

Готов поспорить, вы даже ни разу не видели этой формулы.
Эта очередная формула площади треугольника, применяется
в крайне редких случаях — когда известны два угла и сторона,
к которой эти углы примыкают.

Как найти площадь треугольника

Различных формул, которые дают возможность вычислить площадь фигуры с тремя углами, достаточно много. Поэтому вы сами можете выбрать ту, по которой вам будет это легче сделать. Прежде чем с ними познакомиться, нужно определиться с некоторыми обозначениями:

S – так обозначается площадь фигуры;

a, b, c – обозначение его сторон;

h – значение высоты многоугольника;

p– значение полупериметра;

R – значение радиуса окружности, описанной вокруг нашей фигуры.

Это самые распространенные обозначения, которые можно встретить в формулах, используемых для расчета площади треугольника. Желательно запомнить основные из них, так как это может пригодиться не только во время подготовки к занятиям с вашим ребенком, но и в повседневной жизни. Самая простая формула:

S=1/2*b*h

Немного теории

Как найти площадь различных фигур, проходили еще в начальной школе. Было это давно, так что «обновить» информацию может быть полезно. Будем рассматривать только то, что может иметь отношение к полу. Итак, начнем с самого простого — единиц измерения.

Чтобы посчитать площадь комнаты в квадратных метрах, нужен будет карандаш, рулетка и некоторый багаж знаний

Что такое 1 см² и 1 м²

Площадь любой фигуры измеряется в квадратных метрах или в квадратных сантиметрах. Обозначение см² или м², может встречаться написание кв.м, кв. см., кв. метры, кв. сантиметры и другие вариации.

Что такое один квадратный сантиметр

Один квадратный сантиметр — это площадь квадрата со стороной 1 см. Если нарисовать такой квадрат, стороны которого равны 1 см, то заштрихованная часть (на рисунке красным или синим) и будет один квадратный сантиметр. Соответственно, квадрат со стороной один метр — 1 м — имеет площадь один квадратный метр. Тот самый «квадрат площади». То есть, это квадратный участок пола (или стены) со стороной в один метр — 1 м².  В одном квадратном метре десять тысяч квадратных сантиметров: 1 м² = 10000 см².

Формулы

Это то, что касалось единиц измерения и их соответствия. Но наши помещения, слава богу, больше чем один квадратный метр. Как посчитать площадь комнаты? Сколько в ней квадратных метров? Обычно комната имеет форму прямоугольника, реже — квадрата. Значит, надо будет вспомнить формулы нахождения площади квадрата и прямоугольника.

При помощи очень простых формул, можно рассчитать площадь прямоугольника и квадрата

Надо длины сторон прямоугольника перемножить. Получим искомую площадь. Давайте потренируемся.

1. Имеем прямоугольник со сторонами 80 см и 50 см. Перемножаем эти цифры: 80 * 50 = 4000 см². Это и будет его площадь.
2. Стороны 322 см и 300 см. Получим: 322*300 = 96000 см².
3. Есть квадрат со стороной 60 см. Его площадь — 60 * 60 = 3600 см².

В случае с квадратом длину стороны можно возвести в квадрат — получится одно и то же. Но можно не морочить голову. Проще помнить, что надо стороны умножить.

Простейший калкулятор для расчета площади прямоугольной комнаты.

Перевод квадратных сантиметров в квадратные метры

Когда имеем дело с сотнями сантиметров, удобнее и проще считать в метрах. Мы знаем, что в одном метре сто сантиметров. Давайте решим те же примеры, но переведем сантиметры в метры:

1. 80 см = 0,8 м; 50 см = 0,5 м. Перемножаем 0,8*0,5 = 0,4 м². То есть, 0,4 квадратных метра.
2. 322 см это 3,22 м; 300 см это 3 м. Теперь умножаем полученные цифры: 3,22 * 3 = 9,6 м².
3. 60 см равны 0,6 м. Площадь квадрата с такой стороной 0,6*0,6 = 0,36 м².

Цифры получаются намного меньше, запомнить их проще. И если мы хотим посчитать площадь комнаты в квадратных метрах, ее размеры мы меряем в метрах, а не сантиметрах. Можно перевести квадратные сантиметры в квадратные метры. Как уже говорили, в одном квадратном метре содержится десять тысяч квадратных сантиметров.

Соотношение квадратных сантиметров и квадратных метров

Если же у вас есть площадь в квадратных сантиметрах, чтобы перевести ее в квадратные метры, цифру надо разделить на 10 000. Например:

• 4000 см² / 10000 = 0,4 м²;
• 96000 см² / 10000 = 9,6 м²;
• 3600 см²/ 10000 = 0,36 м².

Как видите, все просто. Надо только запомнить основные положения и посчитать площадь комнаты в квадратных метрах будет совсем несложно. Нужно будет предварительно провести измерения, а потом заняться расчетами.

Подготовка к расчетам

Лазерную рулетку используют в больших помещениях правильной формы

Измеряют линейные величины с помощью рулетки. Можно использовать лазерную рулетку. Прибор показывает точные значения, но применять его можно только на прямолинейных участках, для криволинейных инструмент не пригодится. Подходят линейки длиной 0,5 – 1,5 м.

Правило подготовки к замерам и расчету:

• Выбирают один инструмент. Если берут линейку, пользуются только ей, также поступают с рулеткой. Деления на разных инструментах обычно имеют погрешность, поэтому результаты измерения разными приборами могут отличаться.
• Все промежуточные значения нужно записывать на бумагу. Ручка не всегда пишет из-за пыли в ремонтируемой комнате, поэтому применяют карандаш. Им также ставят отметки на стенах, если протяженности рулетки не хватает на всю длину стены.
• Перед работой план комнаты набрасывают в виде эскиза на бумаге. Это нужно обязательно, если комната имеет сложную планировку, многоступенчатые стены, криволинейные повороты, выступы и ниши.
• Лучше брать рулетку длиной от 5 м, чтобы уменьшить число промежуточных измерений. Для больших объектов, например, галерей, залов, длинных коридоров используют рулетки длиной 10 – 20, но лучше подойдет лазерный инструмент.

Свойства треугольника

1. длина любой стороны треугольника меньше суммы длин двух остальных сторон, но больше разницы длин двух остальных сторон;
2. высота треугольника образует прямой угол со стороной, к которой проведена;
3. площадь треугольника равна половине произведения длины высоты треугольника и длины стороны, к которой проведена высота S_ABC=a⋅h/2.

Пример. Можно ли построить треугольник из отрезков с длинами: 3 см, 7 см, 4 см?

Необходимо вспомнить следующее правило: если сумма любых двух сторон меньше либо равна оставшейся стороне, то треугольник построить не получится. 3 + 4 = 7, значит построить треугольник не получится.

Пример. Можно ли построить треугольник из отрезков с длинами: 16 см, 32 см, 18 см?

Необходимо вспомнить следующее правило: если сумма любых двух сторон меньше либо равна оставшейся стороне, то треугольник построить не получится. Так как для укаанных длин будут справедливы следующие равенства: 16 + 18 > 32 и 16 > 32 − 18, то треугольник построить получится.

Пример. Можно ли построить треугольник из отрезков с длинами: 1 см, 3 см, 7 см ?

Необходимо вспомнить следующее правило: если сумма любых двух сторон меньше либо равна оставшейся стороне, то треугольник построить не получится. 3 + 1

Пример. Одна сторона, которая образует прямой угол прямоугольного треугольника ABD, равна 4 см, другая сторона, которая образует прямой угол, в 2 раза меньше. Определи площадь треугольника.

Пусть AB = 4 см, тогда сторона BC = 4 : 2 = 2. И тогда площадь треугольника будет равна: S = 2 * 4 : 2 = 4 см2

Одна сторона, которая образует прямой угол прямоугольного треугольника ABD, равна 12 см, другая сторона, которая образует прямой угол, в 3 раза меньше. Определи площадь треугольника.

Пусть AB = 12 см, тогда сторона BC = 12 : 3 = 4. И тогда площадь треугольника будет равна: S = 12 * 4 : 2 = 24 см2

Рассчитай площадь треугольника ABC, если дана площадь клетки — 1 м2.

В треугольнике от вершины B проведём перпендикуляр к стороне AC. Таким образом данный треугольник разбит на два прямоугольных треугольника. Каждый из них — половина прямоугольника.

Поэтому площадь можно рассчитать следующим образом:

S_ABC=4⋅4/2+3⋅4/2=(16+12)/2=28/2=14м2.

Известно, что периметр равностороннего треугольника — 21 см. Определи периметр данного четырёхугольника, который состоит из равносторонних треугольников.

Известно, что периметр равностороннего треугольника — 21 см.

Значит, одна сторона треугольника равна 7 см.

Периметр данного четырёхугольника состоит из 4 таких сторон, значит, равен 28 см.

Дан равносторонний треугольник. 2 раза сделано следующее:

1. на всех сторонах отмечены и соединены серединные точки. 2. На сторонах внутреннего треугольника опять отмечены и соединены серединные точки. Треугольник, который образовался на этот раз, закрашен розовым цветом.

Внутренний треугольник состоит из 4 маленьких треугольников, такими же являются остальные 3 треугольника, следовательно, всего 4⋅4=16 маленьких треугольников.

2. Чему равна площадь большого треугольника, если площадь розового треугольника равна 4 м²?

Площадь большого треугольника равна 16⋅4=64 м².

3. Сколько маленьких треугольников получится, если повторить эти действия (построить такую конструкцию) 4 раза?

Очевидно, что в каждой следующей конструкции число маленьких треугольников увеличивается в 4 раза.

Если повторить эти действия (построить такую конструкцию) 4 раза, то общее число маленьких треугольников будет равняться 256.

4. Сколько маленьких треугольников получится, если повторить эти действия (построить такую конструкцию) 3 раза?

Очевидно, что в каждой следующей конструкции число маленьких треугольников увеличивается в 4 раза.

Если повторить эти действия (построить такую конструкцию) 3 раза, то общее число маленьких треугольников будет равняться 64.

Определи площадь данных фигур, если площадь одной клетки равна 6 см2. 1)

Фигура образует 2 клетки, а ее площадь равна 6 *2 = 12 кв.см.

У второй фигуры будет 8 клеток. Площадь фигуры равна 8 ⋅ 6 = 48см2 .

Подумай, как построены данные фигуры, и определи, сколько клеток будет у следующих двух фигур, если их построить по той же закономерности.

У третьей фигуры — 18 клеток, у четвертой — 32 клетки.

Теорема (формула площади треугольника)

Площадь треугольника равна половине произведения его стороны на высоту, проведенную к этой стороне:

где  — сторона треугольника,  — проведенная к ней высота.

Доказательство:

 Пусть  — высота треугольника (рис. 148). Докажем, что 

Проведем через вершины  прямые, параллельные сторонам треугольника, и обозначим точку их пересечения  Таким образом, мы «достроили» треугольник  до параллелограмма  в котором отрезок  также является высотой, проведенной к стороне 

По формуле площади параллелограмма  Треугольники  равны по трем сторонам (у них сторона  общая,  как противолежащие стороны параллелограмма). Эти треугольники имеют равные площади. Тогда площадь треугольника  составляет половину площади параллелограмма 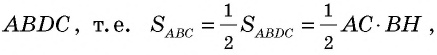 что и требовалось доказать. 

Следствие 1

Площадь прямоугольного треугольника равна половине произведения его катетов:

где  — катеты прямоугольного треугольника.

Действительно, в прямоугольном треугольнике высота, проведенная к катету, совпадает с другим катетом.

Следствие 2

Площадь ромба равна половине произведения его диагоналей:

где  — диагонали ромба.

Действительно, диагонали делят ромб на четыре равных прямоугольных треугольника с катетами  (рис. 149). Используя следствие 1, имеем:

Следствие 3

Площадь равностороннего треугольника со стороной  вычисляется по формуле

Обоснуйте это следствие самостоятельно.

Опорная задача

Медиана делит треугольник на два равновеликих треугольника. Докажите.

Решение:

Пусть  — медиана треугольника  (рис. 150).

Проведем высоту  треугольника  Этот отрезок является одновременно высотой треугольника  проведенной к стороне  и высотой треугольника  проведенной к стороне  Учитывая равенство отрезков  имеем:

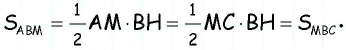
Эта задача имеет интересные обобщения: если высоты двух треугольников равны, то отношение площадей этих треугольников равно отношению их оснований; если основания двух треугольников равны, то отношение площадей этих треугольников равно отношению их высот.

Докажите эти утверждения самостоятельно.

Рекомендую подробно изучить предметы:

Геометрия Аналитическая геометрия Начертательная геометрия

Ещё лекции с примерами решения и объяснением:

• Соотношения между сторонами и углами произвольного треугольника
• Окружность и круг
• Описанные и вписанные окружности
• Плоские и пространственные фигуры
• Взаимное расположения прямых на плоскости
• Треугольник
• Решение треугольников
• Треугольники и окружность

Как посчитать квадратные метры

Время от времени перед нами встаёт проблема, как посчитать квадратные метры: при расчёте оплаты за коммунальные услуги или во время ремонта, когда нужно посчитать, сколько рулонов обоев нужно, чтобы обклеить стены, или сколько банок краски.

На самом деле, все эти данные указаны в техническом паспорте, где дана чёткая планировка квартиры, указано количество квадратных метров каждой комнаты и общая площадь квартиры.

Как посчитать квадратные метры стен

Если же паспорта нет, а вам всё равно нужно узнать, например, как посчитать квадратные метры стен, то сделать это, на самом-то деле, не так сложно. Для этого вам понадобятся школьные знания геометрии. А именно – формула площади прямоугольника S= a*b. То есть, вам нужно высоту ваших стен помножить на ширину. Для этого нужно сделать следующее:

1. Измерить ширину стены. Лучше всего это делать по линии пола или потолка, так как эти линии наиболее перпендикулярны.
2. Изменить высоту стены. Это расстояние от пола до потолка. Как правило, в «хрущёвках» это 2,5 м, в «брежневках» – 3 м, в «сталинках» – 3,5 или 4 м. Но лучше всего измерить самостоятельно, чтобы не прогадать.
3. Узнать площадь. Полученные величины следует перемножить между собой – и у вас есть сумма квадратных метров одной стены.
4. Сумма площадей. Так как в комнате не одна стена, а четыре, то те же операции нужно проделать с остальными стенами, а потом сложить полученные 4 площади. В итоге у вас будут квадратные метры стен всей комнаты.
5. Вычесть излишки. В каждую комнату есть, как минимум, один вход. В современных квартирах очень модны перепланировки с разными арочными и другими проёмами. Естественно, если вам нужно рассчитать количество рулонов обоев, то это расстояние вам не нужно. Поэтому измеряете высоту и ширину проёма, перемножаете их и полученное число вычитаете из общего количества метров стен.

Как видите, ничего сложного в этом нет. Если вас интересует, как посчитать квадратные метры комнаты, то это ещё проще.

Как посчитать квадратные метры комнаты

Основная формула всё та же. Только теперь нам нужны длина и ширина пола.

1. Измеряем ширину. Если у вас вдоль стены стоит мебель, не стоит сразу же её куда-то перетаскивать. Вы вполне можете измерить ширину по стене или потолку – комната же состоит из прямоугольников, и параллельные стороны у него равны.
2. Измеряем длину. Измеряем смежную стену/пол/потолок.
3. Находим площадь. Перемножаем полученные цифры – и всё.

Если вам нужно посчитать квадратные метры всей квартиры, тот принцип тот же: считаем каждую комнату, коридорчики и кладовки, а потом всё вместе складываем.

Вот так всё просто.

Для чего необходимо знать площадь комнаты и что потребуется для расчетов?

В каких же случаях необходимо рассчитывать площадь комнаты?

Конечно, в первую очередь для определения количества расходных материалов для ремонта. Многие закупают их с запасом, а излишки возвращают в магазин. Однако в данном случае теряется много времени, к тому же не все магазины предоставляют такую услугу. Поэтому целесообразней правильно высчитать площадь всех поверхностей перед покупками.

Чтобы у вас не осталось много обрезков, правильно рассчитайте площадь стен, которые требуют оклейки

• Кроме того, зная площадь, проще распланировать свой бюджет. Ведь даже стоимость работ наемных работников в большинстве случаев зависит от того, сколько квадратных метров они должны обработать.
• Количество осветительных приборов также зависит от площади. Однако в большинстве случаев к сложным расчетам при выборе светильников не прибегают, данный вопрос обычно решается опытным путем.

Пример недостаточного освещения в ванной комнате

И последнее. Одна из главных величин в квартире – объем помещений (при этом необходимо площадь умножить на высоту), ведь в зависимости от него подбирают климатическое оборудование.

Мощность кондиционера в первую очередь зависит от объема помещения

Таким образом, существует огромное количество причин, по которым необходимо правильно высчитать площадь помещения. Но с чего же начать? Сначала нужно подготовить измеряемое помещение и инструменты.

Измерения желательно проводить в полностью освобожденном помещении. Если такой возможности нет, расчистите хотя бы участки около стен, ведь именно вдоль них будут проводиться замеры.

Обязательно отодвиньте всю крупную мебель от стен, которые вы будете измерять

Итак, для определения площади помещения необходимы следующие приспособления:

1. Рулетка. Конечно, электронное приспособление удобней, но оно имеет большую погрешность. Кроме того, такой рулеткой не измерить сложные формы, при работе с выступающими элементами также могут возникнуть проблемы. Поэтому оптимальный набор – простая рулетка и линейка. Главное – проверить их точность, так как многие старые или детские приспособления имеют приличную погрешность.
2. Карандаш.
3. Листок бумаги для вычислений и записи результатов.
4. Калькулятор.

Кроме того, вам может понадобиться длинная линейка для проверки ровности стен.

Треугольник

Треугольник является базовой фигурой геометрии, встречающейся повсеместно. Расчет всех геометрических фигур и тел основаны на наличии в них тех или иных треугольников, благодаря чему становится возможным применить множество теорем и формул, несвойственных конкретным фигурам по отдельности. Равносторонние треугольники, равнобедренные треугольники и прямоугольные треугольники составляют каркас решения геометрических задач, и обладая множеством дополнительных построений внутри треугольника, они предоставляют огромное количество значений тех или иных длин. Все биссектрисы, медианы, высоты, радиусы окружностей, вписанных или описанных около таких треугольников, можно рассчитать в этом разделе через геометрический калькулятор. Для этого необходимо ввести любые имеющиеся вводные данные, и калькулятор выдаст не только значения всех остальных параметров треугольника, но и объяснит преобразования формул, использованные для этих расчетов.

Зная: Стороны треугольника	Зная: Два угла и сторону треугольника	Зная: Два угла и сторону треугольника «A»
Зная: Две стороны и угол треугольника	Прямоугольный треугольник	Зная: Катет и гипотенуза прямоугольного треугольника
Катет «B» и гипотенуза прямоугольного треугольника	Зная: Катет и угол прямоугольного треугольника	Катет «A» и угол «β» прямоугольного треугольника
Катет «B» и угол «α» прямоугольного треугольника	Катет «B» и угол «β» прямоугольного треугольника	Зная: Гипотенузу и угол прямоугольного треугольника
Гипотенуза и угол «β» прямоугольного треугольника	Равнобедренный треугольник	Зная: Высоту и сторону равнобедренного треугольника
Высота и сторона «B» равнобедренного треугольника	Зная: Сторону и угол равнобедренного треугольника	Сторона «A» и угол «β» равнобедренного треугольника
Сторона «B» и угол «α» равнобедренного треугольника	Сторона «B» и угол «β» равнобедренного треугольника	Зная: Высоту и угол равнобедренного треугольника
Высота и угол «β» равнобедренного треугольника	Равносторонний треугольник	Зная: Площадь равностороннего треугольника
Зная: Высоту равностороннего треугольника	Зная: Радиус вписанной окр. равностороннего треугольника	Зная: Радиус описанной окр. равностороннего треугольника
Зная: Основание и высоту треугольника

Прямоугольная комната

Приступаем к расчетам. Повторение – мать учения, поэтому для тех, кто забыл, как считать площадь комнаты и ее периметр, напомним курс пятого класса.

К примеру, имеем типовую прямоугольную комнату с шириной равной 2,5м и длиной, равной 4 м. Тогда, площадь равна длине, умноженной на ширину, или 2,5 х 4 =10 м2 . Периметр в нашем примере равен сумме длин всех сторон или 2,5 + 4 + 2,5 + 4 = 13м.

Значит для натяжного потолка вам надо заказать пленку размером 10 м2 и приобрести профилей суммарной длины 18 + 20% (на обрезку) = 15,6 м. Естественно, при покупке багетов надо округлить суммарную длину до значения, кратного длине одной планки. Если в магазине имеется двухметровый профиль, то потребуется купить 16 м или 8 планок.

Расчет по высоте

Найти площадь равностороннего треугольника можно также, если известна его высота и сторона. Половина длины высоты умножается на сторону, выбрана может быть любая высота и сторона, ведь согласно свойствам, они все одинаковые: , где a – это длина стороны. Ее легко запомнить, однако, на практике она применяется достаточно редко.

Если в задаче указана информация о том, что треугольник является равносторонним и известна величина высоты. А чему равна длина стороны неизвестно, то можно воспользоваться формулой, позволяющей ее рассчитать. Найти сторону можно разделив двойную величину высоты на корень квадратный из трех, математически выглядит следующим образом: . После этого применяется формула площади, где расчеты производятся через сторону, она описана в предыдущем пункте.

Для того чтобы не делать лишних расчетов можно вывести формулу этого показателя сразу же через высоту. Квадрат высоты делится на корень квадратный из трех. Она будет выглядеть так: . В этом случае можно не применять формулу равнобедренного треугольника через сторону.

Вычисление площади треугольника по его стороне и высоте

Для чего нужно знать площадь помещения

Первая причина проведения замеров и соответствующих вычислений — покупка строительных и отделочных материалов. Площадь пола потребуется для приобретения ламината, линолеума, ковролина. Подготовительные работы в виде стяжки, установки лаг, выравнивания основания также потребуют знания квадратуры.

Для стен считают количество штукатурки, шпаклевки, обоев. Объем краски, грунтовки также рассчитывают по отношению к квадратному метру.

Причины для нахождения площади внутренних поверхностей:

• Проверить расчеты наемных работников. Часто они считают квадратуру всех отделочных работ на начальном этапе, когда на стенах нет выравнивающего слоя по маякам, чистовой шпаклевки. После проведения всех этих работ квадратура обоев и покраски значительной уменьшится.
• При закладывании проводки на освещение. Определяют количество светильников в соответствии с номами освещенности.
• Площадь важна при установке отопительных агрегатов, разводке радиаторных контуров. По показателям выбирают мощность приборов вентиляционной системы.

Часто приходится высчитывать площадь помещения?

Часто
62.5%

Редко
37.5%

Одни раз измерил и записал
0%

Проголосовало: 8

Вычисление площади прямоугольной комнаты

Помещение, не имеющее никаких, даже небольших, выступов и ниш или, попросту говоря, прямоугольное – самый простой вариант для снятия мерок и подсчета значений площади. Здесь достаточно вспомнить самую простую формулу из курса математики – как рассчитывается площадь такой фигуры, как прямоугольник. Для этого необходимо измерить лишь ширину (А) и длину комнаты (B). Таким образом, мы получаем, что S (площадь) будет равна значению, которое будет получено в результате перемножения двух показателей А и В.

Расчет площади прямоугольной комнаты

Результаты всех измерений указываются в метрах. После запятой указываются сантиметры. Например, длина стены получилась 376 см, тогда получается (в 1 м – 100 см), что длина этой стены будет равна 3 м 76 см.

Меряем прямоугольный пол

Если в комнате есть камин, то нужно посчитать его площадь и отнять от получившейся цифры. Ведь под камином напольное покрытие укладываться не будет. Конечно, если речь не идет о демонтаже этого сооружения.